Optimizing the data cache performance  
------- Taking advantage of locality in matrix multiplication

When we dealing with multiple arrays, with some arrays accessed by rows and some by columns. Storing the arrays row-by-row or column-by-column does not solve the problem because both rows and columns are used in every iteration of the loop. We must bring the same data into the cache again and again if the cache is not large enough to hold all the data, which is a waste. We will use a matrix multiplication (C = A.B, where A, B, and C are respectively m x p, p x n, and m x n matrices) as an example to show how to utilize the locality to improve cache performance.

 

1. Principle of Locality

Since code is generally executed sequentially, virtually all programs repeat sections of code and repeatedly access the same or nearby data. This characteristic is embodied in the Principle of Locality, which has been found empirically to be obeyed by most programs. It applies to both instruction references and data references, though it is more likely in instruction references. It has two main aspects:

1. Temporal locality (locality in time) -- individual locations, once referenced, are likely to be referenced again in the near future.
2. Spatial locality (locality in space) - references, including the next location, are likely to be near the last reference.

Temporal locality is found in instruction loops, data stacks and variable accesses. Spatial locality describes the characteristic that programs access a number of distinct regions. Sequential locality describes sequential locations being referenced and is a main attribute of program construction. It can also be seen in data accesses, as data item are often stored in sequential locations.

• Taking advantage of temporal locality

When instructions are formed into loops which are executed many times, the length of a loop is usually quite small. Therefore once a cache is loaded with loops of instructions from the main memory, the instructions are used more than once before new instructions are required from the main memory. The same situation applies to data; data is repeatedly accessed. Suppose the reference is repeated n times in all during a program loop and after the first reference, the location is always found in the cache, then the average access time would be:

t_a = (n*t_cache + t_main)/n = t_cache + t_main/n

where n = number of references. As n increases, the average access time decreases. The increase in speed will, of course, depend upon the program. Some programs might have a large amount of temporal locality, while others have less. We can do some optimization about this.

• Taking advantage of spatial locality

To take advantage of spatial locality, we will transfer not just one byte or word from the main memory to the cache (and vice versa) but a series of sequential locations called a block. We have assumed that it is necessary to reference the cache before a reference is make to the main memory to fetch a word, and it is usual to look into the cache first to see if the information is held there.

 

2. Data Blocking

For the matrix multiplication C = A.B, if we made code as below:

For (I = 0; I < m; I++) 
    For (J = 0; J < n; J = J++) { 
        R = 0; 
        For (K = 0; K < p; K++)             
           R = R + A[I][K] * B[K][J]; 
        C[I][J] = R; }

The two inner loops read all p by n elements of B and access the same p elements in a row of A repeatedly, and write one row of n elements of C. The number of capacity misses clearly depends on the dimension parameters: m, n, p and the size of the cache. If the cache can hold all three metrics, then all is well, provided there are no cache conflicts. In the worst case, there would be (2*m*n*p + m*n) words read form memory for m*n*p operations. 

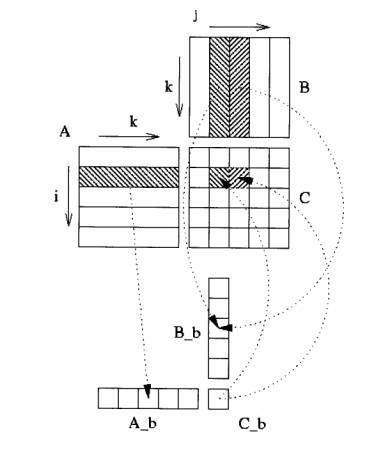
To enhance the cache performance if it is not big enough, we use an optimization technique: blocking. The block method for this matrix product consist of: 

• Split result matrix C into blocks C_I,J of size N_b x N_b, each blocks is constructed into a continuous array C_b which is then copied back into the right C_I,J. 
• Matrices A and B are spit into panels A_I and B_J of size (N_b x p) and (p x N_b) each panel is copied into continuous arrays A_b and Bb. The choice of N_b must ensure that C_b, A_b and B_b fit into one level of cache, usually L₂ cache. 

Then we rewrite the code as:

For (I = 0; I < m/N_b; I++){
   A_b = A_I;
   For (J = 0; J < n/N_b; J++) {
      B_b = B_J; C_b = 0;
      For (K = 0; K < p/N_b; K++)
         C_b = C_b + A_bK*B_Kb;
      C_I,J = C_b; }}           here "=" means assignment for matrix 

We suppose for simplicity that N_b divides m, n and p. The figure below may help you in understanding operations performed on blocks. In the case of previous algorithm matrix A is loaded only one time into cache compared to the n times access of the original one, while matrix B is still accessed m times. This simple block method greatly reduce memory access and real codes may choose by looking at matrix size which loop structure (ijk vs. jik) is best appropriate and if some matrix operand fits totally into cache.

In the previous we do not talk about L₁ cache use. In fact L₁ will be generally too small to handle a C_I,J block and one panel of A and B, but remember that operation performed at C_b = C_b + A_bK*B_Kb is a matrix-matrix product so each operand A_bK and B_Kb is aceessed N_b times: this part could also use a block method. Since N_b is relatively small, the implementation may load only one of C_b, A_bK, B_Kb into L₁ cache and works with others from L₂.

 

 

Presented by: Hongqing Liu, Stacy Weng, and Wei Sun