Lab 26: Enforcing Data Definitions
Implement this lab in typed racket.
Getting Typed Racket Running
In order to create a Typed Racket program, you will need change the language. To do this, create a new program, open the Choose Language menu item in DrRacket. Choose "The Racket Language". This will add #lang racket to the top of your file. Edit the line to be #lang typed/racket.
As mentioned in lecture, Typed Racket, unlike ISL+ and friends, does not have a testing framework built-in. So we will be using the rackunit library.
The following will import check-equal?, roughly analogous to check-expect from ISL+, from rackunit. We do this in the context of a test submodule, which is the idiomatic way of adding tests to Racket and Typed Racket programs:
#lang typed/racket (module+ test (require/typed rackunit [check-equal? (Any Any -> Any)]))
You can now write functions and tests like this:
(: sqr : (Number -> Number)) ;; Square the given number. (module+ test (check-equal? (sqr 5) 25) (check-equal? (sqr -5) 25)) (define (sqr x) (* x x))
Choose the initial Head and Hands, and get started!
Typed Interactions
Once you’ve switched the language to Typed Racket, try some expressions in the interactions window.
> 0 - : Integer [more precisely: Zero]
0
OK, so we’ve only tried 0 so far, but there’s a lot going on. Typed Racket informs us of the type of every expression we type into the interactions window. For zero, it informs us that 0 is an Integer, but more precisely has the type Zero. It’s useful to have a very specific type for Zero, so it can be used easily in other data definitions.
Ex 1: Do all numbers have their own type? Try out some other examples to find out. You should find at least one number with another very specific type.
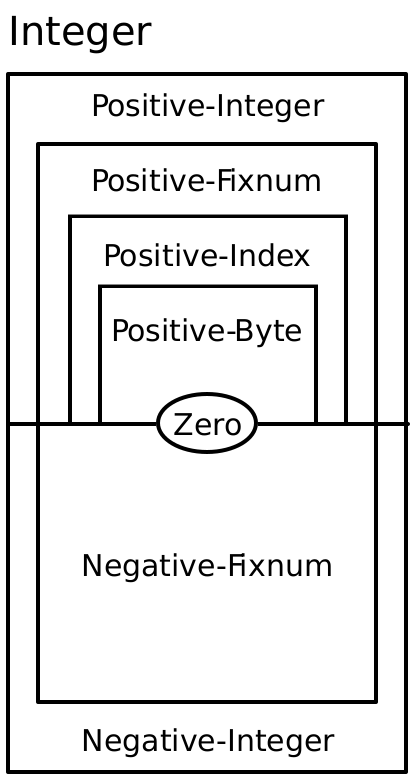
Ex 2: As detailed in the Assignment 10: Typing Markup specification, the numbers we’ve been using in class are very sophisticated compared to most programming languages. What types do each of the numbers 1, 10, 100, 1000, ... 1000000000000 have? Find one number for each of the types given in the image below:
Look at the Type Reference for more details about the distinctions between these types, if you’re interested. Most of the time we can use the type Real in the same way as we used the data definition Number to date.
Ex 3: Test other atomic values that you’ve used in the student languages; write down what types Typed Racket ascribes to them in a comment.
Function Types
Now let’s type some anonymous functions in the interactions window.
> (lambda (x) x) - : (-> Any Any)
#<procedure>
This looks right, given Any value that function just returns that same value. The -> type constructor is how function types are expressed. As with most expressions we’ve seen in this class, it is a prefix operation. The last argument given to -> is the output and the rest of the arguments are the inputs.
Ex 3: Write down (in a comment) types for functions that:
accept a number and return a string,
accept two strings and return a number,
accept no arguments and return a Positive-Integer.
> (lambda (x) (if (zero? x) 1 (sub1 x))) eval:1:0: Type Checker: type mismatch
expected: Number
given: Any
in: x
Hmm, this was rejected. Let’s see what the issue is:
> zero? - : (-> Number Boolean)
#<procedure:zero?>
OK, the function zero? only accepts values of type Number. The Type Checker claims that we gave it a value of type Any. Because we gave the argument x no type, it could be anything! Without any ascribed type, an anonymous function we write assumes its arguments can be of Any type. That would break the contract for =.
Ex 4: Properly annotate the argument x with a valid type to satisfy the Type Checker. Look at the Typed Racket guide if you are unsure of the proper syntax.
Ex 5: Write down two examples of functions that are rejected by the Type Checker. Did you find any functions that you’d like to be able to write that you were unable to write?
More Complex Types
Whenever we’ve needed to hold onto more than one piece of data at once, we’ve defined structures to do so. When we’ve needed a type that can describe more than one kind of data, we used an enumeration data definition. For example, we can make binary trees with numbers at the leaves:
(define-struct leaf (val)) (define-struct node (left right)) ; A Tree is one of: ; - (leaf Number) ; - (node Tree Tree)
We can do the same in Typed Racket, but the data definition is defined as a type.
In Typed Racket, we write a similar implementation, but define a type rather than write a data definition. Note that the implementation refers to the type, and the type refers to the names of the structs that make up the implementation.
(struct leaf ([val : Number])) (struct node ([left : Tree] [right : Tree])) (define-type Tree (U leaf node))
The structures look very similar, but their fields have annotated types. The type Tree is defined as the union of the leaf and node types. That union is described by the type constructor U.
Ex 6: Design the function tree-height that given a Tree, returns the height of that Tree.
Ex 7: Design the function tree-product that given a Tree, returns the product of all the leaves of that Tree.
Ex 8: Design a data type STree for binary trees with strings at the leaves. Design a function tree->stree that maps number->string over a Tree, returning an STree of the same form.
Ex 9: It will be a pain to define a different *Tree type for every kind of value. Design a new parameteric type constructor Treeof and new structure definitions for leaves and values. The leaf structure must be able to hold a value of any type. Refer to the struct and define-type documentation to see how parameterized structures and types are defined.
Ex 10: Design a more general tree-map using your parameterized tree from Ex 9.
Ex 11: Implement a function ntree->stree that maps a [Treeof Number] to a [Treeof String] using tree-map.