Lab 21: Generating Fractals
Implement this lab with the Intermediate Student Language with Lambda.
Make sure you follow The Style we use for the {B,I,A}SL{,+} languages in this class.
Choose the initial Head and Hands, and get started!
Warm-up with Circles and Spirals
Let’s begin by drawing some circles. Before we start, here is a bit of setup code:
(require 2htdp/image) (require 2htdp/universe) ; Constants (define WIDTH 300) (define HEIGHT 160) (define MT (empty-scene WIDTH HEIGHT)) ; next-size : Number -> Number (define (next-size s) (/ s 2))
This is our first target image.
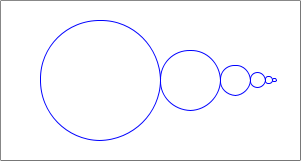
The circles get smaller as they move to the right.
Ex 1: Design a function circles that takes two numbers x, size, and an image img. If size is less-than or equal to 2, then your function returns img unchanged (base case). Otherwise, your function should place a circle on the recursive result where x is shifted by (+ size (next-size size)), size is (next-size size), and the original img.
Ex 2: Adjust next-size so that it divides by 3/2 (or something a bit smaller), instead of 2. Modify WIDTH so you get something like the image below.
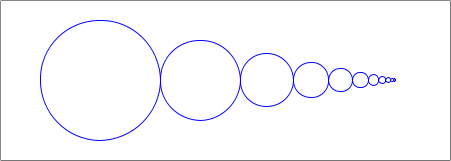
Ex 3: Define a similar function spiral that takes four numbers and an image img. In addition to x and size, the function also takes y and ang, which represent the center y coordinate of a circle, and the current angle (in radians).
Hint: In your recursive call to spiral, you must update x and y based on your (or your partner’s) knowledge of trigonometry:
next-x = x + (size+nextsize) * cos(ang),
next-y = y + (size+nextsize) * sin(ang).
You can also add to the ang. Try (/ pi 10). Using that as the initial angle should give you something like the image below.
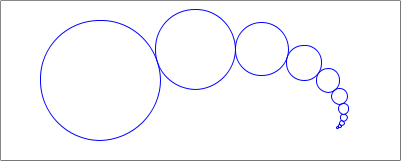
Ex 4: Modify the various parameters to your function to get interesting results. For example, if you modify the function to be structurally recursive (using sub1 instead of next-size), and draw the same size circles each time (be sure the function terminates!), you might get something like the image below.

Trees
Swap Head and Hands!
Now that we’re warmed up, let’s implement a few generative fractals. First up is a simple "tree" fractal.
Here’s some helper code to get you started:
; put-line : Number Number Number Number String Image -> Image ; Put a line on the image starting at (x, y) len distance in the given ; direction with the given color. (define (put-line x y ang len color img) (place-image (line (* (cos ang) len) (* (sin ang) len) color) (+ x (* (cos ang) (/ len 2))) (+ y (* (sin ang) (/ len 2))) img))
Ex 5: Design the function tree that takes four numbers, x, y, ang, and len and draws a tree on a given image. If the len is less than 3, then the function just puts a line at x/y/ang/len of some color (like "green") into the image.
Otherwise the function puts a "brown" line at x/y/ang/len, and recur twice: once with x/y placed one third up the trunk at an angle off to the left, and another with x/y placed two thirds up the trunk at an angle off to the right. The length should be cut in half.
Hint: One of the recursive calls should be calculated as follows:
next-x = x + len/3 * cos(ang),
next-y = y + len/3 * sin(ang),
next-ang = ang + pi/3,
next-len = len/2.
The other recursive call should use ang - pi/3, at 2*len/3 away.
You should be able to easily modify the parameters to get various images.


Koch Snowflake
Swap Head and Hands!
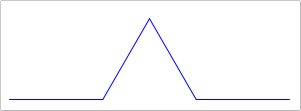
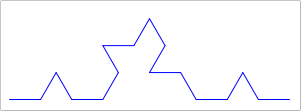
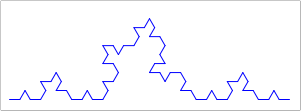
Ex 6 Similar to the tree fractal, we can do interesting things by changing recursive calls. The Koch snowflake is an interesting recursive fractal. Design the function koch that takes the same arguments as tree, with an additional iter parameter. Like in the last lab, iter tracks the number of remaining iterations.
For each iteration you cut the line into three pieces and make four recursive calls. The key insight is that you should only draw a line when the number of remaining iterations reaches 0. The images below show the first 4 iterations and a more elaborate version (bigger, with 6 iterations), of a "snowflake" variation that (I think) looks pretty cool. See if you can emulate it, or come up with something better!