


Next: Prove or Disprove the
Up: bool
Previous: bool
Suppose that each of the variables below represents a single
bit. Rewrite the expression using either a minimum of
C-bitwise operators or a minimum of operands or both. Trust me-solutions exist. Note that logical OR operator is indicated by the
plus symbol, so that  means A OR B. The logical
AND is 'assumed' when two symbols are written together, such
as A AND B is written as
means A OR B. The logical
AND is 'assumed' when two symbols are written together, such
as A AND B is written as 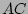 . The logical XOR function is
the
. The logical XOR function is
the  , giving
, giving 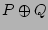 for P XOR Q. Finally, the apostrophe
represents logical NOT. You get to use the symbols
for P XOR Q. Finally, the apostrophe
represents logical NOT. You get to use the symbols
~ \ & | ^ , the bit-wise C operators.
-
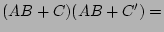
-
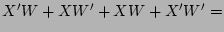


-

-
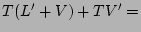

-
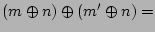
-
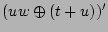
-

-
![$[(x+a)(x+b)(x+c)(x+d)]'=$](img15.png)
MM Hugue
2008-01-27