CMSC330
NFA and DFA
NFA and DFA
NFA and DFA
NFA and DFA
So far we have only really looked at DFAs
DFA: Deterministic Finite Automata
Easy to check regex acceptance
But machines hard to create
But machines hard to create
Here is /(a|b)*abb/'s DFA
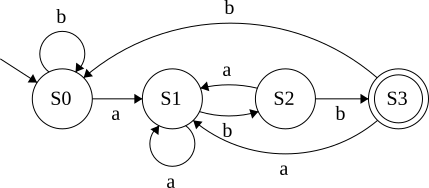
We can create NFA much easier
We can create NFA much easier
NFA: Nondeterministic Finite Automata
Harder to check regex acceptance
Machine easier to make
Machine easier to make
Here is /(a|b)*abb/'s NFA


- Multiple transitions on same symbols
- Many ways to accept
- Can have epislon (\(\epsilon\)) transitions

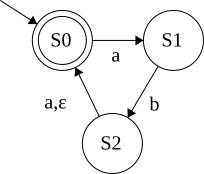
First: define a FSM
- Alphabet (\(\sum\))
- Set of States (\(Q\))
- Start State (\(q_0 \in Q\))
- Final States (\(F \subseteq Q\))
- DFA Transitions (\(\delta: Q \times \sum \mapsto Q\))
- NFA Transitions (\(\delta: Q \times (\sum \cup \{\epsilon\}) \mapsto Q\))
Accepting with DFA is easy

Accepting with NFA is hard

Accepting with DFA is easy
Accepting with NFA is hard
Good news: can convert between NFA and DFA
with the help of regex
All DFAs are NFAs
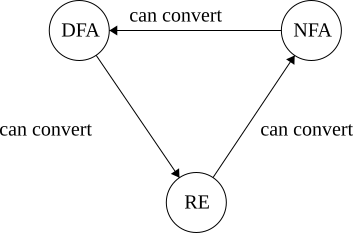
Regex to NFA
NFAs are easy to build: start here
Regex to NFA is dependent on what we need for Regex
- Alphabet
- Concatenation
- Union
- Kleene Closure
\(\emptyset\): The language is null
\(\epsilon\): empty string
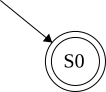
\(\sigma\): A letter in the alphabet

Concatenation: \(\{xy\vert x \in L_1 \land y \in L_2\}\)

Concatenation: \(\{xy\vert x \in L_1 \land y \in L_2\}\)

Union: \(\{x\vert x \in L_1 \lor x \in L_2\}\)
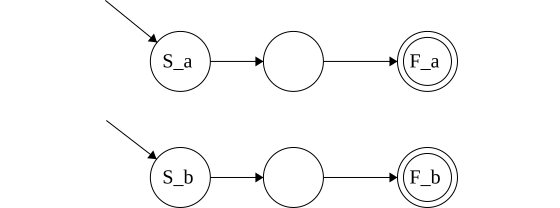
Union: \(\{x\vert x \in L_1 \lor x \in L_2\}\)
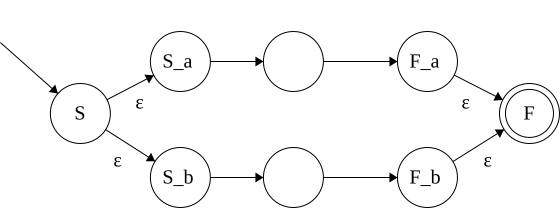
Kleene Closure: \(\{x\vert x \in \{\epsilon\} \lor x \in L_1 \lor x \in L_1L_1 \lor \dots\}\)

Kleene Closure: \(\{x\vert x \in \{\epsilon\} \lor x \in L_1 \lor x \in L_1L_1 \lor \dots\}\)

NFA to DFA
NFAs: hard to check acceptance
DFAs: easy to check acceptance
Convert from NFA to DFA
Basis: combine states to represent possible NFA states
(ie. Make a state that represents "could be in S1 or S2")
Basis: combine states to represent possible NFA states
Subset Algorithm
Requires two Functions:
- \(\epsilon\)-closure
- Move
Basis: combine states to represent possible NFA states
Subset Algorithm
Requires two Functions:
- \(\epsilon\)-closure
- Which states can I get to using only \(\epsilon\) transitions
- Can always reach self
- Move
- Which states can I get to using one symbol transition
- Could be none
\(\epsilon\)-closure
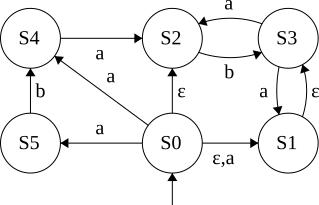
Reached: S0
\(\epsilon\)-closure

Reached: S0,S1
\(\epsilon\)-closure

Reached: S0,S1,S2
\(\epsilon\)-closure

ReachedL S0,S1,S2,S3
\(\epsilon\)-closure
NFA = (alphabet, states,start,finals,transitions)
e-closure(s)
x = s
do
s= x
x = union(s,{dest|src \in sand (src,e,dest) in transitions})
while s!= x
return x
Move

Reached: S1
Move

Reached S1,S4
Move

Reached S1,S4,S5
Move

Reached S1,S4,S5
Just go through transition list
Putting it all together
NFA = (a, states, start,finals,transitions)
DFA = (a, states, start,finals,transitions)
visited = []
let DFA.start = e-closure(start), add to DFA.states
while visited != DFA.states
add an unvisited state, s, to visited
for each char in a
E = move(s)
e = e-closure(E)
if e not in DFA.states
add e to DFA.states
add (s,char,e) DFA.transitions
DFA.final = {r| s \in r and s \in NFA.final}
DFA to Regex
Regex\(\Rightarrow\)NFA\(\Rightarrow\)DFA
Time for DFA\(\Rightarrow\)Regex
Idea: remove states and replace with Regex
Each state has 3 parts: incoming,self, outgoing
Regex added in that order


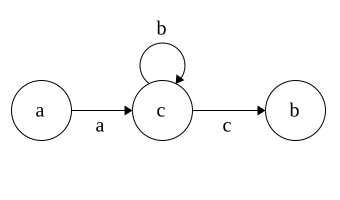

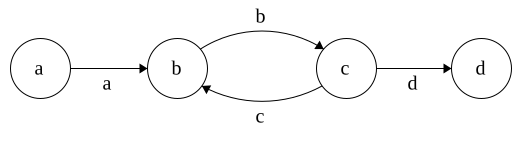
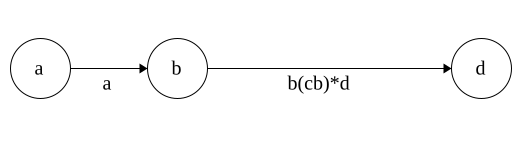

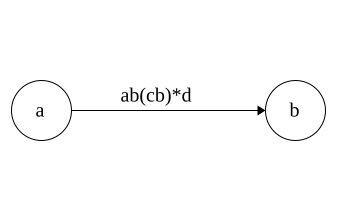
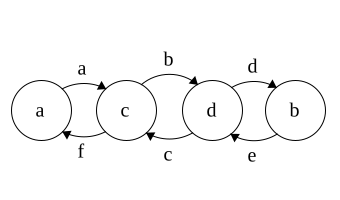
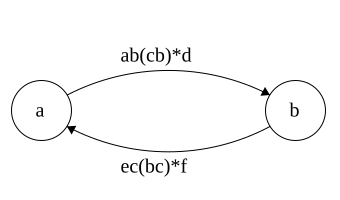
Note: This is incomplete