This document discusses the historical and current research in the area of fire simulation, and describes some basic concepts for generating fire in 3D Studio Max. Also available in PDF.
Introduction
Fire as Texture
Physical Models of Fire
Relevant Features of 3D Studio Max
Particle System Flame
Conclusion
References
Fire’s basic components can be described as follows:
These components determine the appearance of fire. Their interaction results in all types of fire, from calm candle flames to roaring forest fires.
In the field of computer science, fire’s complexity is still an elusive problem. Many attempts have been made to model fire, both for visual and functional purposes, with increasingly successful results. The approaches have been rather diverse, but can be subdivided into attempts to model fire as a texture, and the use of physical formulas to simulate its behavior. This paper presents a survey of existing research into fire representations and the fundamental components of 3D Studio Max that can be used to create animated fire simulations.
The basic motivation for wanting to model fire as a texture that can be applied to a 3D object is the speed and ease of subsequent use. In general, textures are either image-based or procedural. Image-based textures map points from 2D images onto 3D surfaces. Procedural textures are generated by “combining noise into various mathematical expressions” [Perlin 1999]. They require no source images and, therefore, need very little memory. Furthermore, they can be used to “carve out” an object from texture material, rather than distorting a 2D image. Procedural textures (also called solid textures), produce much more realistic results for natural textures such as marble and metals. Procedural textures can also be animated over time. In the 1980’s Perlin was the primary contributor to the creation of procedural textures and the algorithm for generating Perlin noise. Perlin and Hoffert presented several methods for creating procedural fire, using noise to generate turbulence in the texture [Wei et all 2002].
More recent textures have increased in complexity, tackling the problem of animation over time in various ways. [Wei et al. 2002] combined elements of texture with physical concepts. Expending on the work of [King et al. 2000], which proposed the use of texture splat primitives to simulate fire, they described a method for letting the splats interact with the environment. Using the Lattice Boltzmann Model from fluid mechanics, [Wei et al. 2002] allowed their display primitives to follow a simple physical model that lends itself to real-time computation. A texture splat is a small image of a fire detail with a Gaussian filter applied for smoothness where it overlaps other splats. The color and transparency of the splat are calculated according to its position in the fire. Both the movement of the splats and the number of primitives necessary for the animation are rather limited, greatly increasing efficiency over particle system methods, discussed in the following section.
[Neyret 2003] suggested a method for making animated fluids, such as fire, that exhibit realistic flow without requiring the tremendous computational power necessary to calculate formulas of fluid dynamics. This texture animated both the overall movement of the flow as well as small-scale swirling by simulating a low resolution fluid and letting it advect a specific texture. The challenge was in preserving space and time continuity while maintaining the statistical properties of the texture in a specified range. There are three basic methods for animating textures: simple advection of the parametric space, relying on particles instead of simple parameterization to control the location of texture patterns (similar to the method proposed by Wei, above), and introducing time as a fourth dimension in the texture parameters. [Neyret 2003] describes these approaches more specifically and points out the failings of each. His improved method involves “locally adapting the texture latency…, blending the procedural noise in frequency space…, and defining a control mechanism for small scale animation” and allows for creating visually high-resolution textures without a dramatic increase in processing power.
Models that have attempted to simulate fire using physical formulas have approached the task from different directions that have recently converged. Several groups of researchers have focused on fire’s behavior. Their simulations were intended for training and prevention purposes and aimed to predict fire’s precise interaction with its environment. Others focused on the visual elements of fire, trying to create visual realistic for use in games and movies.
Recently, fire prevention and suppression agencies have started relying on computer-generated fire simulations to help understand and predict the growth and spread of fire. These are modeled with one of two types of models – zone or field. Zone models divide the space into one hot upper and one cool lower control volumes. Although these models cannot account for complex geometries in a room and are not useful for prediction, they are computationally simple and very effective for reconstruction of fires. Field models, also known as computational fluid dynamics (CFD) models, divide the space into many homogenous cells. Although these models produce very accurate results, the computations involved tend to be rather lengthy due to the large numbers of elements. More importantly, these models generate large volumes of output data that must be interpreted. [Govindarajan et al. 1999] go on to suggest a visualization method to view the results of multiple CFD model runs simultaneously.
[Zaniewski and Bangay 2003] proposed using extended Lindenmayer Systems, rather than CFD, to model fire propagation and geometry inside an enclosed building. Their model also predicted where and how fast fire is most likely to spread, thus helping to identifying the safest parts of the building. L-Systems, commonly used to model individual plants and entire ecosystems, had not been used to store information about fire. In 2001, Devlin and Chalmers conducted research into the impact of different fuels on the color of flames [Nguyen et al. 2002].
On the other side of the spectrum, researchers have used physical formulas, or simplified variants thereof, to produce realistically looking, rather than behaving, fire. Used for artistic purposes, emphasis in these models has been placed on ease of control by the animator. [Reeves 1983] was the first to simulate fire using particle systems. He proposed using clouds of primitives to define an object’s volume, rather than polygons to define its surface. These new objects were dynamic, since particles can move, change size, be created or destroyed, and had non-deterministic shapes with fuzzy boundaries.
More recently, research has focused on gaseous “blobs,” rather than simplistic particles, whose density is advected (i.e. displaced) and diffused by wind fields over time. [Stam and Fiume 1995] implemented a “fire model for a fuel map defined on solid objects, [which] corresponds to non-burning objects coated with a flammable substance.” Their algorithm can be summarized as follows:
for each time frame do
for each solid object in the scene do
Update temperature of the object
Generate flame blobs and update fuel map
end
for all flame blobs do
Update temperature and density
Generate smoke blobs
Move and diffuse
end
for all smoke blobs do
Update density
Move and diffuse
end
end
Relying on the physical properties of fuels and the impact of heat on the movement of gas, they were able to model the appearance of flames and the location of smoke. They also proposed a method for warping the gas blobs to produce less regular, more believable shapes.
Extending on these ideas, [Beaudoin et al. 2001] suggested using individual flames as primitives. Their process was subdivided into three parts: propagation, animation, and rendering of flames. Propagation refers to the spread of flames over a burning object and, in this simplified model, was controlled by fuel density, oxygen supply, wind, and surface orientation relative to gravity. Animation accounts for the deformation of flames placed along a surface, thus capturing the visual dynamics of fire. Each flame primitive is animated, and consists of a chain of connected particles (called the “skeleton”), with the particle adjacent to the surface of the burning object as the root. The rest of the chain moves according to a turbulence vector that is based on user-defined parameters. After being propagated and animated, the flames are rendered into a voluminous mass. To account for the apparent merging of multiple flames, [Beaudoin et al. 2001] proposed the rendering of implicit surfaces to visualize the final fire effect.
By building on physical and graphical models, [Nguyen et al. 2002] achieved the most photo-realistic flames. They divided the model into three distinct visual components: blue flame core, blackbody radiation, and smoke/soot. The core, which gets its blue or greenish color from emission lines of chemical reactions, is modeled as a thin film adjacent to the implicit surface where burning occurs. This surface marks the boundary where oxidized fuel heats up sufficiently to begin combusting. Blackbody radiation produces the yellow-orange color typically associated with flames. The exact color varies with temperature, which must be tracked. As the blackbody radiation diminishes with cooler temperatures, the soot and smoke produced by the flames become visible. Another complexity of the model is the rendering of light emitted by fire. Using the scattering, absorption, and emission properties of fire, Nguyen’s team also accounted for the chromatic adaptation of our eyes to produce fire of the correct colors. In general, this model very successfully simulates fires based on gaseous fuels, but does not wrap around burning objects in as successful an imitation as that of [Beaudoin et al. 2001].
3D Studio Max provides a built-in fire effect that can be rendered on atmospheric apparatus objects. Max allows the animator to choose between tendril and fireball flame shapes, and lets the user choose the inner, outer, and smoke colors. It also takes parameters for flame size, density, detail and number of samples. Although the animator does have options to adjust, the overall effect tends to be “cartoony” and unrealistic. Furthermore, objects with the fire effect cast no light, which must be modeled with a separate light object.
In an attempt to create more sophisticated fire in Max, I used the built-in particle systems. Max supplies two types of particle systems: event driven, and non-event driven. There are four distinct non-event driven systems: Super Spray, Blizzard, PCloud, and PArray, used to simulate fountains, snow/rain, clouds, and the surface of any 3D object, respectively. The creation of particles and the overall shape of the system are controlled by parameters in the emitter. Furthermore, the animator can create space warps (such as wind and gravity) to more finely control the particles’ paths and behavior.
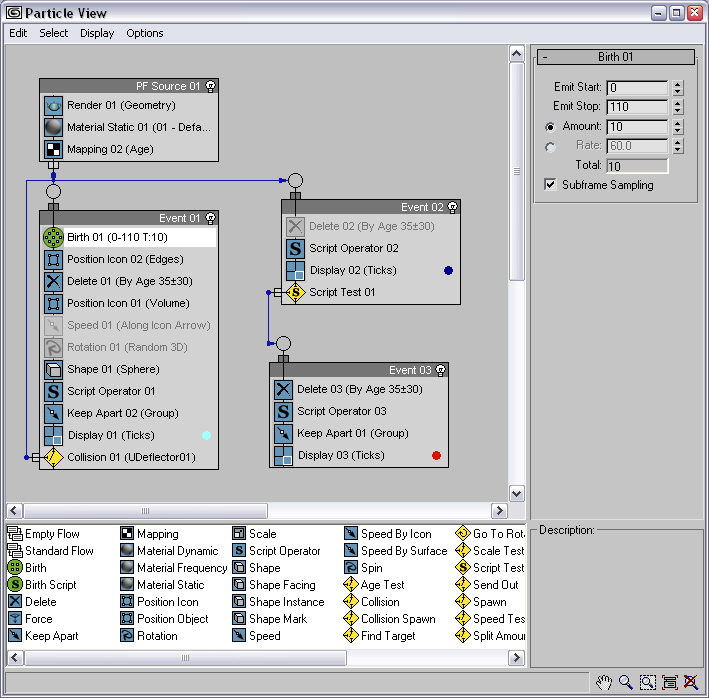
For ultimate control, an animator can use the event-driven particle flow particle system. The particle flow is controlled by a series of events (see Figure 1). Each event can define the size, shape, texture, speed, direction, rotation, and overall behavior of individual particles. Using the birth operator, an animator can defines how many particles may simultaneously exist in a system, what the length of their life spans should be, and on what frame the system should begin and stop emitting. By default, particles are born in Event 01. They can travel between user-defined events by passing predefined tests (such as age or position tests). The most powerful aspect of this system is that Max provides script operators and script tests, allowing the animator to specify behaviors of arbitrary complexity. Max updates the positions of the particles at every frame. To do so, the program sequentially performs all of the operations specified inside an event on the subset of particles that currently belong to that event. Each particle that satisfies the test condition for its current event is moved to the following event, as defined by the animator.

I attempted to use a particle flow to simulate the burning of a candle flame. This process involved modifying the color, position, and movement of the particles. To simulate the color of flames, I gave my particle system a global texture whose diffuse color was a gradient ramp ranging from yellow to red to black. I also added transparency to the texture. Using the material static operator, I mapped particle’s age to coordinates of the texture. As the particles aged, their coloring changed from yellow to red and eventually faded to black smoke.
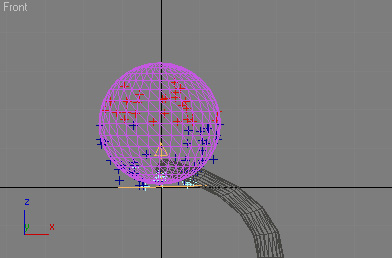
The position and speed of the particles was controlled by three sequential events. Event 1 contained the birth operator and specified that the particles should be emitted upwards with a slight tendency to move closer together. Particles entered event 2 on hitting a non-rendering sphere that served as a deflector. To imitate the fullness at the bottom of a candle flame, the particles skirted around the surface of the sphere up to its equator (see Figure 2). In event 3, the particles’ speed increased and gained a tendency to cluster closer together. I achieved this by adding a “keep apart” operator with a negative value. Finally, to simulate the subtle turbulence of a candle flame, I animated the general path that particles in event 3 followed. I created an object above the particle emitter to serve as the target of the find target test. By animating its x and y coordinates, I was able to simulate the appearance of the flame moving from side to side (see Figure 3). I have not yet added any light to the scene.
One of the major downsides of my model is that, despite its lack of complexity, it is extremely slow. Achieving somewhat realistic results requires thousands of very small particles. Event 2, which calculates the position of each particle by transforming its planar coordinates to polar, adding several degrees to one of the coordinates, and transforming the result back into planar values, is computationally intense. Furthermore, code written in MaxScript is not optimized for mathematical operations (unlike the embedded functions that are created in C++). Therefore, I have noted a variant that produces similar-looking results but renders significantly faster than the above-described approach. The collision test, which normally allows particles to move between events 1 and 2, has several parameters that can influence the behavior of particles upon collision. When particles are set to bounce and slow down after collision, their speed and momentum naturally cause an upward motion. In effect, this combination of settings achieves a result very similar to the manual repositioning of particles around the surface of the sphere, but renders much more quickly.
The problem of fire simulation is rather complex and has been approached from a variety of starting points. The models that achieved the most realistic appearances have been those that have taken the physics of combustion into account by tracking the amount of fuel as well as the temperature of the flames. However, fire simulations serve various functions. For models intended as tools for fire prevention organizations, the realism of the fire’s appearance is secondary. However, rendering the flames is still important as it allows the results of various tests to be more readily interpretable. Also, for animations that must be rendered in real time, the physically based models of fire appearance and propagation are too computationally challenging. Procedural textures, although typically less realistic, are better suited for such tasks. In general, because fire is made of such diverse components as the movement, color, temperature, and transparency of flames, the interaction of flames with the fuel, the production and movement of smoke, light, and the propagation of flames as they engulf and consume objects and oxygen, fire is an extremely difficult phenomenon to simulate fully. But the approaches with the most realistic results have attempted to account for all these factors.
Beaudoin, P., S. Paquet and P. Poulin. 2001. “Realistic and Controllable Fire Simulation.” No description on Graphics interface 2001, 159-166.
Fedkiw, R., J. Stam and H. Jensen. 2001. “Visual Simulation of Smoke.” Proceedings of the 28th International Conference on Computer Graphics and Interactive Techniques, 15-22.
de Goey, L., D. Roekaerts. 2003. Lecture Notes of the J. M. Burgerscentrum Course on Combustion. Ed. K. Schreel. Eindhoven University of Technology, Department of Mechanical Engineering.
Govindarajan, J., M. Ward, and J. Barnett. 1999. “Visualizing Simulated Room Fires.” IEEE Visualization 1999, 475-478.
King, S., R. Crawfis and W. Reid. 2000. “Fast Volume Rendering and Animation of Amorphous Phenomena.” Volume Graphics, 229-242.
Lamorlette, A. and N. Foster. 2002. “Structural Modeling of Flames for a Production Environment.intro Proceedings of the 29th Annual Conference on Computer Graphics and Interactive Techniques, 729-735.
Neyret, F. 2003. “Advected Textures.” Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 147-153.
Nguyen, D., R. Fedkiw, and H. Jensen. 2002. “Physically Based Modeling and Animation of Fire.” Proceedings of the 29th International Conference on Computer Graphics and Interactive Techniques, 721-728.
Perlin, K. 1999. Making Noise. http://www.noisemachine.com/talk1/index.html
Perlin, K. 2003. “Improving Noise.” Proceedings of the 29th International Conference on Computer Graphics and Interactive Techniques, 681-682.
Stam, J. and E. Fiume. 1995. “Depicting Fire and Other Gaseous Phenomena Using Diffusion Processes.” Proceedings of the 22nd International Conference on Computer Graphics and Interactive Techniques, 129-136.
Wei, X., W. Li, K. Mueller, and A. Kaufman. 2002. “Simulating Fire with Texture Splats.” IEEE Visualization 2002, 227-237.
Zaniewski, T. and S. Bangay. 2003. “Simulation and Visualization of Fire using Extended Lindenmayer Systems.” Proceedings of the 2nd International Conference on Computer Graphics, Virtual Reality, Visualisation and Interaction in Africa, 39-48.