In sign magnitude (or signed magnitude), the uppermost or most significant
bit (msb) is referred to as the sign bit. The remaining ![]() bits
are the size or magnitude of the number, with this bit string interpreted
as a
bits
are the size or magnitude of the number, with this bit string interpreted
as a ![]() bit unsigned binary number.
If the sign bit is zero, and
all the other bits are zero, the the number is zero. If the sign bit is
zero, and at least one other bit is non-zero, than the number is positive.
If the sign bit is one, and at least one other bit is one, then the number
is negative. The bit pattern with msb=1 and all other bits zero, is NOT
negative zero; some machines adopt a ``large negative'' value for it, other
machines make it illegal. We will treat it as an illegal bit pattern.
bit unsigned binary number.
If the sign bit is zero, and
all the other bits are zero, the the number is zero. If the sign bit is
zero, and at least one other bit is non-zero, than the number is positive.
If the sign bit is one, and at least one other bit is one, then the number
is negative. The bit pattern with msb=1 and all other bits zero, is NOT
negative zero; some machines adopt a ``large negative'' value for it, other
machines make it illegal. We will treat it as an illegal bit pattern.
Using the notation from the previous section, we have:
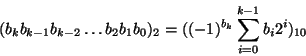
The number ![]() from the previous section requires 13 bits now:
twelve to capture the size or magnitude of the number, and one, the
msb, set to 0, to signify that the number is positive.
from the previous section requires 13 bits now:
twelve to capture the size or magnitude of the number, and one, the
msb, set to 0, to signify that the number is positive.
The negative of ![]() , given by
, given by ![]() matches the previous
value in every bit but the msb, which is now 1 because we are representing
a negative number.
matches the previous
value in every bit but the msb, which is now 1 because we are representing
a negative number.
While this is a nice, logical way of implementing signed integers, if you attempt to add the representations for positive and negative 2087 in base 2, you don't get ``0'', which is the answer in base 10. So, when we want to do arithmetic, we need to move to yet another way of representing integers.