NOTE: The first 6 questions are to be written on paper
and handed it at the beginning of class on Feb 29th. The last question is
a programming assignment that should be turned in by the beginning of class with
the submit program as with the previous assignments.
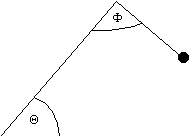
1) Consider a table with a two-dimensional sensing device located at the end of two linked arms. In the figure below, the first arm position is fixed in the bottom lower left corner, and the movable sensor is depicted by the filled dot. Suppose that the lengths of the two arms are fixed, and the arms are connected by simple 1-degree-of-freedom pivot joints. Determine the mathematical relationship between the joint angles Theta, Phi and the position of the sensor. That is, write a function for the position of the dot that is dependent on the joint angles, p(Theta, Phi) given the two arm lengths as constants, a1 and a2.
2) In 3D, show that the following sequences commute using homogeneous coordinate
systems (i.e., T1T2
≡ T2T1):
a) A rotation and a uniform scaling
b) Two rotations about the same axis
c) Two translations
3) In two dimensions, we can write a line as y = mx + h. Find an affine transformation to reflect two-dimensional points about this line. You may leave your answer as a concatenation of the base transforms we have already discussed, but all parameters (such as the amount translated or rotated) must be defined.
4) Devise a test for colinearity of any set of three-dimensional vertices.
5) How are rotation matrices affected if we are working in a left-handed system (instead of a right-handed system) and we retain our definition of a positive rotation (i.e., positive rotation about the z axis moves from the x axis towards the y axis)? Show what the 3D rotation matrix about the z axis will be for a left-handed system.
6) In 3D, show that any sequence of rotations about an axis (around the origin) and translations can be replaced by a single rotation about some vector (around the origin), followed by a translation.
7) Modify your program from Homework #4 to use homogeneous coordinates and matrices, and store your vertices and do the math in three dimensions instead of two. The result should be identical to Homework #4 from the user's perspective until you rotate. You should now allow rotation around any of the three axes which will result in the polygon you draw to be viewed from any 3D viewpoint. In particular, you should:
Implement a general-purpose homogeneous Vector class that contains a 3D homogeneous point or vector.
Implement a general-purpose homogeneous Matrix class that contains an arbitrary 4x4 matrix. It should support matrix multiplication and matrix-point multiplication. It should contain methods for setting the matrix to the Identity matrix, to a general Translation matrix (given translation parameters), a general Scale matrix (given scale parameters), or a general Rotation matrix (given rotation parameters).
When you add points to your polygon, simply set the Z coordinate of each vertex to 0. However, when you transform the points, use the full 3D matrix-point multiplication which may result in the Z coordinate of some vertices being changed (if, for instance, you rotate around the X axis.)
When you render your polygon, simply ignore the Z coordinate of each vertex. This will effectively project your 3D polygons onto the XY plane with an "orthogonal projection".
Modify your interface to allow the user to select whether they are rotating around the X, Y, or Z axes. Then, select the appropriate rotation matrix depending on what the user has selected.