NOTE: The first six questions are to be written on paper and handed it at the beginning of class on Feb 29th. The last question is a programming assignment that should be turned in by the beginning of class with the submit program as with the previous assignments.
1) Remember that we can linearly interpolate from a point P1 to a point P2 with the function
LERP(t, P1, P2) = P1 + t(P2 -
P1)
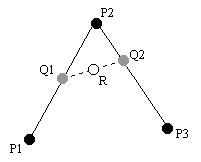
If we have three points P1, P2, P3 as depicted in the figure below, we can simultaneously interpolate from P1 to P2 (call this interpolated point Q1) and from P2 to P3 (call this interpolated point Q2) with the same variable t. We can then use this same variable t to linearly interpolate from Q1 to Q2. That is, when t=0, Q1 and R are at P1, and Q2 is at P2. When t=1, Q1 is at P2, and Q2 and R are at P3. The figure below shows t at value just less than 0.5.
Calculate the formula for the point R. What is the common shape that R follows as t varies from 0 to 1?

2) A fundamental operation in graphics systems is to map a
point (x, y) which lies within a rectangle to a point (xS, yS),
which lies in the viewport of a window on the screen.
If the source rectangle is defined by (xmin, ymin,
xmax, ymax), and the destination rectangle is
defined by (umin, vmin,
umax, vmax).
The result is that (xmin, ymin)
should map to (umin, vmin)
and (xmax, ymax)
should map to (umax, vmax).
Hint: this can be done with a variation of linear interpolation.
Find the mathematical equations that maps (x, y) into (xS, yS). I.e., write xS as a function of x and yS as a function of y.
3) Assume that you have a function that determines whether a point is within a polygon. How would you use that function to determine whether a simple two-dimensional polygon is convex?
4) You are given two vectors, i and j, in 2D that satisfy the following equations: i · i = j · j = 1 and i · j = 0
a. Is there a 2D vector k that is not equal to i so that k · k = 1 and k · j = 0?
b. Is there a 2D vector k so that k · k = 1 and k · j = 0 and k · i = 0?
c. How do the answers to a. and b. change if all the vectors are considered in 3D?
5) Let e1 = (1, 0, 0), e2 = (0, 1, 0), and e3 = (0, 0, 1). Show that if (i, j, k) is equal to (1, 2, 3) or (2, 3, 1) or (3, 1, 2) then ei x ej = ek. Then show that if (i, j, k) is equal to (3, 2, 1) or (2, 1, 3) or (1, 3, 2) then ei x ej = -ek. (Note: this problem is really looking at left and right handed coordinate systems.)
6) Let p1, p2, p3 be points in 3D. Consider the cross product n = (p2 - p1) x (p3 - p1). What does this vector mean geometrically? Let p be any point in the plane spanned by (p2 - p1) and (p3 - p1). What is the geometric relationship between p - p1 and n?
7) Write a Java program that lets you draw an arbitrary polygon and then lets you translate, scale, or rotate that polygon around the origin. Your program should create an interface that lets the user select which of the four modes they are in (drawing, translating, scaling, or rotating). The interface could just be four buttons, or might be a pull-down menu, etc. The program should start in drawing mode. The 4 modes should operate as follows:
Drawing mode: When you first enter this mode, the screen should be cleared. Then, every time you click on the canvas, a point should be added to the polygon and a filled polygon of the points specified so far should be drawn. The points should be stored for use by the other modes.
Translation mode: When you click and drag, the polygon should move with the mouse. Translating should be incremental so that if you click and drag a little bit, the polygon should move a little bit.
Rotation mode: When you click and drag, the polygon should rotate about the origin by the angle specified between the mouse press and the current mouse position. So, if you click at one point and then drag the mouse, the polygon should smoothly rotate about the origin approximately following the mouse.
Scale mode: When you click and drag, the polygon should scale about the origin specified by the distance between the mouse press and the current mouse position.
You are welcome to structure this program any way you see fit, but I would probably implement it by having a data structure which stores the current polygon vertices and the current mode. I'd have the paint method of the panel just draw a polygon that fills in the current vertices. For each mouse event, I would dispatch the event to a method that manages the specific mode. When the event for a particular mode is processed, I would update the vertex list appropriately, adding points in drawing mode, or modifying points with the transformations we studied in class in the other modes. Then, calling panel.repaint() will cause the panel to be repainted, using the current vertex list.