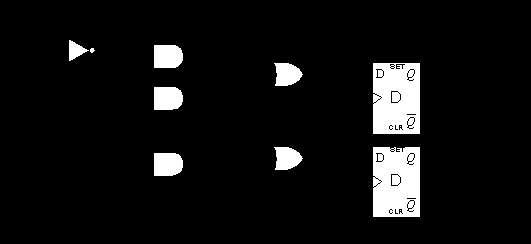
 Logic Diagram:
Logic Diagram:Chapter 4: solutions & guide
Rob Rodgers (
knave@acm.org ) 3-18-1998 CMSC311-Spring 98 (Dr. Hugue)
Assigned problems: 11-22, 24, 25, 27, 30
Additional recommended: Using only combinational logic and D flipflops, construct JK, T and SR flipflops. Then do the same using only T flipflops (make a D). You should also note the behavioral similarities between J-K and S-R flipflops and between a T and J-K flipflop.
!!! PLEASE ATTEMPT TO DO THE ASSIGNMENT BEFORE CONSULTING THE ANSWERS. THINKING ABOUT WHAT THE PROBLEMS WANT YOU TO DO IS 2/3rds OF WHAT YOU’RE LEARNING !!!
Hints: Keep in mind that memorization may not be required, but it can certainly help you work faster. By the time you have done the chapter 4 homework, you should be able to derive the excitation tables from the state tables and the state tables from the excitation tables for J-K, D and T flipflops. Also, know that a D flipflop is very similar to a LATCH.
Material is introduced as necessary.
Printing information: To print these notes, you need to copy this postscript file to the CS cluster machine where your CMSC311 account resides. The easiest way is to use the LYNX character mode web browser. Log into your cluster account and type "lynx
http://www.cs.umd.edu/class" and proceed to the CMSC311 class homework page. Use the arrow keys to highlight this file and press D to download it. You will be asked what you want to do, select save to disk and give it a filename. After saving the file, press ‘q’ then ‘y’ to exit lynx. Finally, use the command "qpr –q csc-ps <filename>" where <filename> is the filename you gave lynx. This will print the file to the CSS building free postscript printer.
Note: I am not repeating the diagrams that are already available. FIRST, get the postscript solutions that are already posted to the web page. Use the same procedure above to download and print the other solutions. I’m going to omit portions of the answers which already appear in the provided files and provide explanations. This file is a SUPPLEMENT to the posted postscript file.
PROBLEM 11
Write the characteristic equations for various flip flops.
What flip flops? What do they do?
Flipflops (except D) differ from the kinds of components we’ve seen until now because their "output" is not directly tied to a specific input line in some formulaic manner, but is instead based on a combination of the current state and, at a clock pulse, the control inputs.
KNOW THESE TWO FACTS:
Fact #1: ALL FLIPFLOPS MAINTAIN THEIR OUTPUT UNCHANGED, WHATEVER THE STATE OF THEIR CONTROL INPUTS, IN THE ABSENCE OF A CLOCK PULSE!
Fact #2: AT A CLOCK PULSE, ALL FLIPFLOPS CHANGE THEIR OUTPUT BASED ON THEIR CONTROL INPUTS AND (except D) ON THEIR CURRENT STATE!
Now, we want to write the characteristic equations. A characteristic equation is the equation that gives the output of the flipflop based on (see above!) the control inputs and the current state. We assume that the state will change only with a clock pulse, and so write the equation for the inputs and outputs when the change occurs. Then we treat the current state (Q(t))as an input, giving us from two to three inputs depending on the flipflop. We always have one output.
So, we have a set of inputs and a set of outputs. WHAT DO WE DO?
Right: a truth table. Let’s do them.
JK
Inputs: Q(T), J, K
Outputs: Q(t+1)
|
J |
K |
Q(T) |
Q(T+1) |
observed |
|
0 |
0 |
0 |
0 |
J, K = 0, no change |
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
K = 1, set to 0 (reset) |
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
J = 1, set to 1 (set) |
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
J and K, complement |
|
1 |
1 |
1 |
0 |
Q(T+1) = JQ’+K’Q
SR
Inputs: Q(T), S, R
Outputs: Q(t+1)
|
S |
R |
Q(T) |
Q(T+1) |
observed |
|
0 |
0 |
0 |
0 |
S, R = 0, no change |
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
R = 1, set to 0 (reset) |
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
S = 1, set to 1 (set) |
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
X |
S AND R = ILLEGAL!! |
|
1 |
1 |
1 |
X |
ILLEGAL STATE!! |
Q(T+1) = S+R’Q
Note that not all input combinations are allowed with an SR flipflop but that it resembles a JK in all other cases. An SR flipflop does not contain the complement operation. Since an SR is so close to a JK, we could BUILD an SR with a JK simply by adding a few AND and NOT gates. Try it.
(hint: if you see SandRandQ(t) you want to get a zero out. You can get a zero out by setting an SR’s control inputs to S=0 R=1. Same logic applies to the 0 to 1 complement operation.)
D
Inputs: D
Outputs: Q(t+1)
|
D |
Q(T) |
Q(T+1) |
|
0 |
D.C. |
0 |
|
1 |
D.C. |
1 |
Q(t+1) = D
Do not be confused by D flipflop trickery! What differentiates the D flipflop from a straight wire or buffer is that the output of the flipflop changes ONLY AT A CLOCK PULSE! If the D is set to 1 it will continue to output 1 FOREVER no matter WHAT you set the D line to unless there is a clock pulse!
A D is as close as we get in CMSC311 to a latch. Since we know that all flipflops are made of latches, we should be able to build ANY flipflop out of a D flipflop. Try it.
T
Inputs: Q(T), T
Outputs: Q(t+1)
|
T |
Q(t) |
Q(t+1) |
observed |
|
0 |
0 |
0 |
T = 0, no change |
|
0 |
1 |
1 |
|
|
1 |
0 |
1 |
T = 1, invert |
|
1 |
1 |
0 |
Q(t+1) = TQ’ + T’Q (which is T xor Q)
Note again that without a clock pulse, the flipflop wont invert no matter what you set T to.
PROBLEM 12
Given:
DA = X’Y + XA
DB = X’B+XA
Z = B
 Logic Diagram:
Logic Diagram:
Truth table:
Just plug in the possibilities. Remember, current states are inputs. Because one of our equations relies on more than one of the flipflops, we need to merge them into one big table. Here is the merged truth table for the formulas.
Inputs:
Ain Q(t) for D flipflop A
Bin Q(t) for D flipflop B
X, Y inputs
Outputs:
Aout Q(t+1) for D flipflop A (used internally!)
Bout Q(t+1) for D flipflop B (used internally and externally)
Z taken from B out, same as last B state (Q(t) for B)
|
Ain |
Bin |
X |
Y |
Aout |
Bout |
Z |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Now we need to draw a state diagram. How do we do this? We’ll use the binary # given by A & B as our state NUMBER. For convenience, we’ll add to this number the value of Z. Then, if A and B are both "0", our Z must also be 0 (since the output when A and B are in this state is 0). Likewise, when A is 0 and B is one, we’ll call this state "1/1" since Z is also 1.
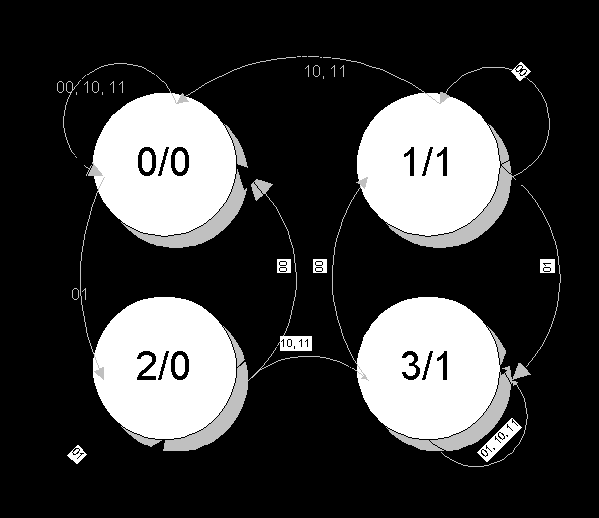 Now we need a state diagram. Group your states and give inputs:
Now we need a state diagram. Group your states and give inputs:
PROBLEM 13
Given:
Da = ( BC’ + B’C)X + (BC+B’C’)X’
Db = A
Dc = B
What does this MEAN? It means that we’re wiring the output of A and B to the inputs of B and C. In other words,
Da = ( BC’ + B’C)X + (BC+B’C’)X’ (where B, C are the current/last states for the flipflops)
Db = A_current/last_state
Dc = B_current/last_state
Part (a) asks us to derive the state table for the circuit. This is given in the provided postscript file. As before, our current states are INPUTS as is our input, X.
Part (b) asks us to draw the state diagram, one for X = 0 and one for X = 1. (in .ps). Notice that in the table, 000 always goes to 000 when X = 0 and 111 always goes to 111 when X = 1. These states rely totally on X – the flipflops in our circuit will hold in 000 or 111 until the necessary X input is given and a clock pulse occurs to cause them to begin changing states again.
PROBLEM 14
Once again we are asked to derive a state table and diagram for the provided sequential circuit. (Both are in .ps). This time the problem includes a full adder.
We know that a full adder has the following table, giving us S and C based on inputs XYC (the diagram is unclear on this last point: the line labeled "Z" is the input carry line and it comes from the output of the D flipflop).
As a reminder:
FULL ADDER:
|
X |
Y |
Cin |
Sum |
Cout |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
But Cin equals the output of our D flipflop, which is . . . . RIGHT! Q(t). Then we create a table as
|
X |
Y |
Q(t) |
Q(t+1) |
S |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Since we have 1 flipflop, we have TWO states, 0 and 1. We have TWO inputs so each of our transitions will be labeled with TWO inputs. See the ps file for the final diagram.
PROBLEM 15
We’re supposed to trace the outputs for an input sequence. Do problems like this by simple brainless "follow the inputs." In this case, the state machine in the diagram takes one input and has one output (given at the state change). Thus, a transition from 00 to 01 has an output of 0, as does a state change from 00 to 00.
Here’s what happens:
|
string: |
present state: |
resulting state: |
output: |
|
0 |
00 |
00 |
0 |
|
1 |
00 |
01 |
0 |
|
0 |
01 |
00 |
1 |
|
1 |
00 |
01 |
0 |
|
1 |
01 |
11 |
0 |
|
0 |
11 |
00 |
1 |
|
1 |
00 |
01 |
0 |
|
1 |
01 |
11 |
0 |
|
1 |
11 |
10 |
0 |
|
0 |
10 |
00 |
1 |
|
1 |
00 |
01 |
0 |
|
1 |
01 |
11 |
0 |
|
1 |
11 |
10 |
0 |
|
1 |
10 |
10 |
0 |
|
0 |
10 |
00 |
1 |
PROBLEM 16 and 17
Table 4-4 gives us a state table for 2 JK flipflops (A and B) and one input. It includes the JK flipflop inputs.
FACT: a state table IS the state machine!
A state diagram is just a handy, human-readable way to make its behavior a little easier to work with.
Working this problem out. We know we have two flipflops, so we can have at most 2^2 = 4 states in our state diagram. We can see that all four states actually occur (is this necessarily true?) from the table. Also, we are not concerned with any output.
Thus we draw 4 state circles and label them 0, 1, 2 and 3. These are our states, and they are given in the table by the value of the binary number define by A,B.
Lastly, we need to connect the states. Algorithm:
FOR EACH line in the state table given, DRAW AN ARC from the PRESENT STATE to the NEXT STATE and label it with the value of X for that line.
Problem 17 asks us simply to draw the circuit defined by the table. See the postscript file for the diagram and circuit.
PROBLEM 18
We are asked to derive the state table and diagram for a circuit. How do we do this?
Right: Truth table.
What are our inputs? We see that we have two flipflops, each of which takes two inputs, and another input labeled X. But we can also see that out J & K control inputs for the first flipflop (on the left) take as their input the OUTPUTS (q and q’) of the second flipflop (on the right).
What does this mean? It means that the J input for the left flipflop is the Q(t) for the right flipflop, and that the K input on the left flipflop is Q(t)’ for the right flipflop.
Since our states are ALREADY listed as inputs in the state table, this should present no problems, and in fact, does not.
What about the right flipflop? We can see that BOTH the J and K flipflops are ties to an XOR gate that connects to X (our only free input) and A (which is Q(t) for the left flipflop).
One thing to observe here is that, for the right hand flipflop, either both inputs are 1 or both are 0. But we know that if Q(t) for ANY jk flipflop is 0, the resulting state is given by J. Conversely, if the Q(t) for ANY jk flipflop is 1, the resulting state is given by K, so we also know that it DOESN’T MATTER that both J and K are identical. Just something to remember.
Now, with what you have you should be able to construct the state table. You can add an empty column for the output (which is an XOR of the Q(t) for the right and (Q(t)-right XOR X)) since determining the output is only a matter of plugging the inputs into the formula (above) after determining the Q(t+1) states for both flipflops. In other words, it can be done after the rest of the table is finished.
Having done the table, draw 4 empty state circles (two flipflops = at most four states) and label them 0 through 3. Follow the algorithm for problem 17 to read the state transitions off of the state table and complete your diagram.
Diagram & table are given in the postscript file.
PROBLEM 19
We are asked to build another more complex circuit that uses two JK flipflops (A and B) and two inputs (X and Y). We are also given an output, Z, which is NEVER DEFINED IN THE PROBLEM. Can you do the problem? No.
READ THE FOLLOWING:
The definitions for the inputs to Ja, Ka, Jb and Kb are CORRECT.
Let "A" = Q(t) for flipflop A
Let "B" = Q(t) for flipflop B
Then Z is defined as: XYA + X’Y’B
!! STOP HERE and ATTEMPT THE PROBLEM !!
Solving the problem.
The diagram and truth table are given in the postscript file.
You may be noticing that the process of generating state tables and diagrams is very mechanical. This is exactly true. The more mechanical and automatic you make it, the easier you will find problems. Even complex problems can be approached in the piecemeal fashion of simply drawing the table, then identifying the states and then drawing the state diagram from the table.
PROBLEM 20, 21
Problem 20 is another "design a sequential circuit" question. However, this time the approach is less rote. We are told the behavior we want from the circuit and asked to implement it.
Given: two D flipflips, A and B, and an input, X.
Goal: Design a circuit s.t. when X = 0, the state of the circuit remains the same, and when X = 1, the circuit proceeds through states in the following way: 0->1->3->2->0.
Let’s restate that: Design a circuit that maintains its state while X = 0, but changes states (on clock pulses) when X = 1.
That’s a little different, isn’t it?
What we are being asked to do in this problem is exactly the same as deriving an excitation table for a flipflop such as a J-K. Instead of deriving or being given a table, we are being asked to create one.
Let’s consider a circuit that transitions between two states, 0 and 1, on every pulse. Designing such a circuit with a D flipflop is EASY:
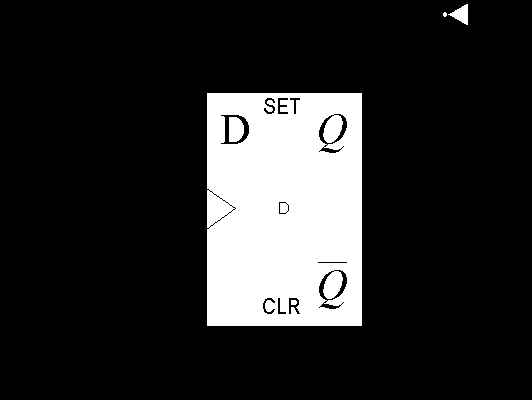
The above circuit transitions between 1 and 0 on every clock pulse (try it and see).
But suppose we wanted something more. That’s easy, too, once you get the hang of it. It begins by writing a state table. First, write the first three columns of our state table for our above circuit. We have two inputs, the states of our D flipflops A and B, and one input, X. So for the first three columns, use A, B and X and fill them out from 000 to 111.
Now we want to add two columns which are our "outputs" – that is, our Q(t+1) states for A and B. But instead of doing what we’ve done before, instead of DERIVING our new states from our inputs and old states, this time we’re going to ASSIGN our new states as we choose.
That is, because we WANT our states not to change for all of the lines where X = 0, just copy the Q(t) states for Q(t+1) states for A and B. Now, for each of the X = 1 states, fill in the A and B states WE WANT for the Q(t+1) states.
Now, what we’ve constructed is a perfectly good state table. Does it represent some circuit? You bet it does. It must. Anything we can express in a COMPLETE truth table is a constructable circuit.
Now, the question is, how do we GET that circuit? And here is the answer:
WE KNOW WHAT WE HAVE (the inputs available, the first three columns of our table), and WE KNOW WHAT WE ARE (for each flipflop, we know the state we have going into the clock pulse, as it’s given in the A or B left-side column of the truth table), and WE KNOW WHAT WE WANT.
So, let’s take the question of the following line in the table:
Inputs outputs
|
A |
B |
X |
A |
B |
|
0 |
0 |
1 |
0 |
1 |
Now, we consider each flipflop in turn. Ordinarily, we would use a K map for each flipflop to derive simplified equations, but you lucked out and we’re not using K-maps, so we’ll do this with a little brainwork.
We want A to go from 0 to 0 when we see A’B’X. But we know A is a D flipflop and thus it’s output (after a pulse) mimics the input (at the pulse). This, we want to pass 0 into A. If you examine the rest of our table, you will notice that Aout is 1 only when both B and X are 1 or when A is 1 and X is 0. This, the input to A is AX’+BX.
Now derive the input to B.
The proper way to do this problem is to write out the equations that your truth table defines and then to simplify them with Boolean algebra. Consult the postscript file for the final answers, and tables.
PROBLEM 21
Problem 21 is IDENTICAL to problem 20 in procedure. Given the diagram, you can construct the state table for the circuit. Given a state table for a circuit, apply the methods from 18 and 20 to convert the state table into a circuit. See the postscript file for the final input equations.
(Basically, there is no need to actually draw the circuit, since you should be able to construct any circuit given the formulas by now. The important thing is to be able to derive the equations. Recommended: draw the circuit anyway.)
PROBLEM 22
Problem 22 concerns constructing a JK flipflop from a D flipflop and combinational logic. Before we can do that, we need to have the equations for the D flipflop input and outputs.
What we are designing is a little circuit that should be able to drop in wherever we se a JK flipflop. A JK flipflop has two control inputs, J and K. So we’ll take those two inputs and use them for our own purposes. Additionally, we have a D flipflop, which has a single input, but doesn’t do anything with that input but copy it. Since the D flipflop’s Q(t+1) state does not rely on its q(t) state, it IS UNIQUE AMONG THE FLIPFLOPS WE HAVE STUDIED and we DO NOT USUALLY USE ITS CURRENT STATE IN OUR STATE TABLE.
BUT!! We want to model a JK flipflop, which DOES depend on the current state of the flip flop to provide the complement capability. Thus we DO, IN THIS CASE, PUT THE Q(T) STATE FOR THE D FLIPFLOP IN OUR TABLE!
Thus, the first three columns of our table look like this:
|
J |
K |
Q(t) |
Q(t+1) |
|
0 |
0 |
0 |
? |
|
0 |
0 |
1 |
? |
|
0 |
1 |
0 |
? |
|
0 |
1 |
1 |
? |
|
1 |
0 |
0 |
? |
|
1 |
0 |
1 |
? |
|
1 |
1 |
0 |
? |
|
1 |
1 |
1 |
? |
And now we want to follow what we did for question 20, that is, write in the Q(t+1) that we want in the "new state" column. From the characteristic equation for the JK flipflop, which is:
Q(T+1) = JQ’+K’Q
Plugging them in, we get:
|
J |
K |
Q(t) |
Q(t+1) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Now we follow the procedure from 20 and 21 to derive the formula, simplify, and we have our newly invented JkfromD flipflop:
Din = Dout’J + DoutK’
Which should look, well, eerily familiar. Wondering what’s going on here?
PROBLEM 24
Problem 24 introduces a new flipflop called a JN flipflop. You are asked to derive the characteristic equation for a JN flipflip and told that N = K’.
This should be a no-brainer. Just do exactly as we’re told: write out the state table for a JK flipflop, invert the K column, and label it N. Write the Boolean equations, simplify. Derive the state table:
|
J |
N |
Q(t+1) |
action |
|
0 |
0 |
0 |
reset (set to 0) |
|
0 |
1 |
Q |
maintain |
|
1 |
0 |
Q’ |
complement (invert) |
|
1 |
1 |
1 |
set to 1 |
PROBLEM 25
An excitation table represents the how inputs affect the current state. We can construct it directly from the answer to 24. We construct it as follows:
1. Write a column for our current state
2. Write a column for our desired state
3. Write a column for each of our inputs
4. Choose the inputs to change column 1 into column 2
|
Q(t) |
Q(t+1) |
J |
N |
|
0 |
0 |
0 |
X |
|
0 |
1 |
1 |
X |
|
1 |
0 |
X |
0 |
|
1 |
1 |
X |
1 |
This table is almost identical to the excitation table for a JK flip flop. What’s changed? In the rows where the JK flipflop "listens" to the K line, it now gives the behavior of K’. If you complement the last two lines of the table for the "N" you will produce a JK flipflop table.
PROBLEM 27
Problem 27 asks us to design a circuit for the state diagram on page 218. Note that this is the same diagram that we used for #21, so we can take the state table for #21 and convert it to a circuit once we find the inputs. Find the inputs using the methods discussed in previous problems. As before, it is not necessary to actually draw the circuit (but it is good practice) once you have found the input equations. You can find the input equations as before.
This problem uses JK flipflops instead of D flipflops. You still need two flipflops.
Inputs:
Ja = BoutX
Jb = Bout’
Ka = Aout’X’
Kb = AoutX’
PROBLEM 30
This problem is IDENTICAL in almost every way to problems 20 and 21. Consult the instructions. Your goal is to find the input equations, which are:
Ja = E(BX+B’X’)
Ka = E(BX+B’X’) (the same!)
Jb = E
Kb = E