Problem 1: `` Buzzin' in 3-Space" (36 pts)

(6) 1.1

Build a K-D tree from the set of points below using the following assumptions:

• the points are inserted in alphabetical order by label
• the x coordinate is the first key discriminator
• if the key discriminators are equal, go left

A:	(0,7,1 )	B:	(1,2,8)	C:	( 6, 5,1)
D:	(4,0,6 )	E:	(3,1,4)	F:	( 4, 0,9)
G:	(9,9,10 )	H:	(3,4,7)	I:	( 1, 1,1)

(6) 1.2

Explain an algorithm to identify all points within a k-d tree that are within a given distance, 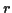$r$, of the point 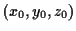$(x_0,y_0,z_0)$. Your algorithm should be efficient, in the sense that it should not always need to examine all the nodes.

(6) 1.3

The three-dimensional analog of a point-quadtree is a point-octree. Give an expression for the minimum number of nodes in a left complete point-octree with levels numbered $0,1, \ldots, k$.

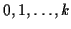(6) 1.4

Explain the difficulties, if any, with deletion of nodes in a point octree. Hint: One way that deletions are performed is by re-inserting any nodes in the subtrees of the deleted one. Why?

(6) 1.5

Describe a set of attributes of the data set, or any other reason, that would cause you to choose a k-d tree over a point-octree, and explain your reasoning. Or, if you can't imagine ever choosing the k-d tree instead of the point-octree, explain why.

(6) 1.6

Describe a set of attributes of the data set, or any other reason, that would cause you to choose a point-octree over a k-d tree for three dimensional data, and explain your reasoning Or, if you can't imagine ever choosing the point-octree instead of the k-d tree, explain why.