Social Worksheet 1
Summer 2015
Dr. Michelle McElvany Hugue
Some of the following statements are True; others, woefully, are False. Your job is to circle T or F as appropriate. You will receive two points for each correct action. For an additional point on false items, briefly explain why the statement is false.
Unless otherwise stated, assume that ![]() refers to the number of keys present in the structure.
refers to the number of keys present in the structure.
- 1
- T F A k-ary tree is a finite set of elements that is either
empty or consists of a root with k disjoint subsets, each a
k-ary tree.
True-it's the definition direct from the glossary.
- 2
- T F An 8-way search tree has keys in the leaves.
True-in fact all the nodes in a search tree contain keys.
- 3
- T F Each external node of an extended k-ary tree
can have up to k children.
False: Every node in a k-ary tree has space reserved for k children or k child pointers. However, an extended k-ary tree is created by replacing the empty child pointers in the k-ary tree with pointers (or references) to another type of node-called an extender-which is terminal. That is, the leaves of an extended k-ary tree do not have children. Often a lightweight pattern is used, wherein the extenders refer to a singleton nil ( empty) object. So, extenders either correspond to an empty node, an existing object; or, a new object, all terminal. The point here is to make some kind of notation which indicated that the leaf nodes have a different role than the internal nodes.
- 4
- T F All nodes in a 5-ary tree have 5 children.
True: All nodes in a 5-ary tree have space for exactly 5 children.
- 5
- T F The amount of space required to store a graph with
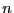 vertices and
vertices and 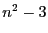 edges is in
edges is in 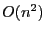
True: Storage is given by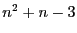 which is in
which is in 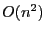
- 6
- T F A tree with all the leaves at the same level is complete.
False: we don't actually use the word tree without a modifier in front of it in this class.However, even if you assumed that we really meant k ary tree, it is still false. Why?
A k-ary tree with all the leaves at the same level will not be complete if the tree is not full as well. A good counter example is a left-complete binary tree where the rightmost leaf is missing (or treated as having a null value in there). It has the same number of internal nodes as the complete tree of the same height (which is full!!), and all leaves at the last (deepest) level, but one fewer leaf node than a complete k-ary tree.
- 5
- T F Every linked list containing keys is ordered.
True: Linked list elements need not be sorted, but the location of the link in the list imposes an ordering on the keys: first, second, third, etc.
- 6
- T F A full 8-ary tree with
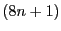 empty child pointers
has exactly
empty child pointers
has exactly 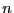 nodes.
nodes.
False: A k-ary tree with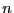 nodes has exactly
nodes has exactly 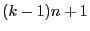 empty child
pointers by the corollary to the full k-ary tree theorem. So, if
empty child
pointers by the corollary to the full k-ary tree theorem. So, if
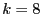 , we must have
, we must have 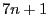 empty
child pointers present for
empty
child pointers present for 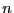 nodes. If
nodes. If 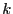 is 9, then the number of
empty child pointers is
is 9, then the number of
empty child pointers is 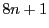 . Note that it is still false if
the term
full is deleted.
Why? Because full k-ary trees with n nodes are in the set of all
k-ary trees.
. Note that it is still false if
the term
full is deleted.
Why? Because full k-ary trees with n nodes are in the set of all
k-ary trees.
- 7
- T F Storage for a PR octree with a maximum of
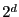 by
by
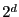 by
by 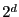 unit cubes is in
unit cubes is in 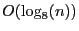 .
.
False: Because each three dimensional key requires exactly one leaf node, and it can be shown that the maximum number of gray nodes grows linearly with the number of keys, giving, storage for the PR octree in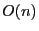 .
.
- 8
- T F The keys in a max heap are maintained in
order according to the BST property.
False: The keys in a max heap are removed in descending key order, but need not be maintained that way. The keys in the left and right children of the root of any subtree cannot be larger than the keys in the root. The order of keys in the array that implements the heap is not sorted order, either.
- 9
- T F A single find_key operation for a
PR octree based on a
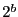 by
by 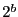 by
by 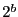 grid of unit cubes is in
grid of unit cubes is in 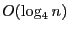 .
.
True: By construction, the maximum number of levels in a PR octree is in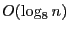 because the level of the deepest key is labeled
because the level of the deepest key is labeled
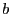 , where
, where 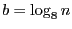 , and the find_key operation must
check at most
, and the find_key operation must
check at most 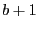 levels. We get the
levels. We get the 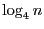 from the change of base formula in Ch2 of Shaffer.
from the change of base formula in Ch2 of Shaffer.
- 10
- T F A PR quadtree with a grid of
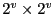 one by one blocks has at most
one by one blocks has at most 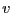 levels.
levels.
False: The number of levels in a PR quadtree with a grid of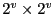 one by one blocks has at most
one by one blocks has at most 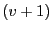 levels.
levels.
- 11
- T F An algorithm with execution time in
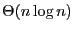 must examine at least
(
must examine at least
(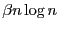 ) nodes, for some positive constant
) nodes, for some positive constant 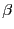 .
.
False: If the time taken by an algorithm is dominated by the time it takes to access a node, then the statement is False because it should say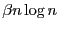 nodes, not at least and not at most. If
the time taken by the algorithm is not dominated by node access time,
then the computation time (comparisons and arithmetic operations)
determine the run time, and no valid inferences about the number of
nodes can be made.
nodes, not at least and not at most. If
the time taken by the algorithm is not dominated by node access time,
then the computation time (comparisons and arithmetic operations)
determine the run time, and no valid inferences about the number of
nodes can be made.
- 12
- T F If
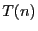 , the
execution time of an algorithm, is in
, the
execution time of an algorithm, is in
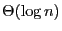 , then there
exist positive constants
, then there
exist positive constants 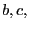 and
and 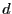 such that
such that
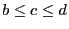 and
and
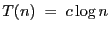 .
sets is finite.
.
sets is finite.
False: Asymptotic complexity is about bounding the behavior of whatever term dominates an expression for time or space as the size of the problem grows. So, there can be all kinds of terms in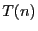 which do not
grow as quickly as
which do not
grow as quickly as 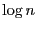 . That is,
. That is,
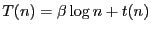 where
where
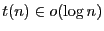 , which means that
, which means that 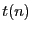 is in
is in 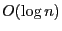 but
not in
but
not in
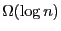 . Thus, equivalently, we might say that the function
. Thus, equivalently, we might say that the function 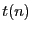 is
only trivially in
is
only trivially in 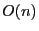 when there exists a constant
when there exists a constant 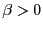 such
that
such
that
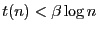 .
.
- 13
- T F All nodes in a k-d tree of
order 6 have 2 children.
True: A k-d tree of order 6 is a binary tree based on the binary search tree property cycling through the coordinate positions of a g-dimensional key.
- 14
- T T Dr. Hugue's favorite beverage is unsweetened iced tea with LOTS of ice.
No excuse if you left this blank.
Next: About this document ... MM Hugue 2015-06-10