


Next: Prove or Disprove the
Up: bool-ans
Previous: bool-ans
-
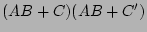
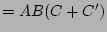 (distributive law (16))
(distributive law (16))
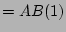 (identity 7)
(identity 7)
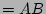 (identity 2)
(identity 2)
A \& B
-
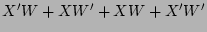
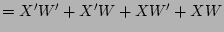 (commutative law (10))
(commutative law (10))
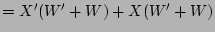 (distributive law)
(distributive law)
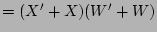 (distributive law)
(distributive law)
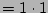 (identity 7)
(identity 7)
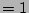 (identity 3)
(identity 3)
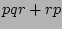
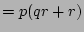 (distributive)
(distributive)
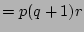 (distributive)
(distributive)
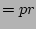 (identity 3)
(identity 3)
p \& r
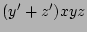
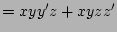 (distributive)
(distributive)
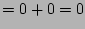 (identity 8)
(identity 8)
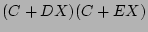
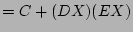 (distributive law (15))
(distributive law (15))
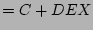 (identity 6)
(identity 6)
C | (D \& E \& X)
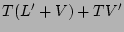
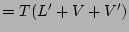 (distributive law)
(distributive law)
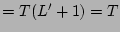 (identities 7 and 3)
(identities 7 and 3)
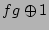
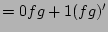 (definition)
(definition)
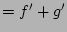 (DeMorgan's law)
(DeMorgan's law)
~f | ~g
-
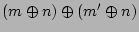
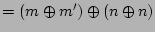 (XOR is commutative & associative)
(XOR is commutative & associative)
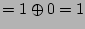 (identities)
(identities)
-
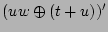
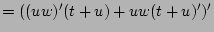 (definition)
(definition)
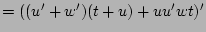 (DeMorgan's)
(DeMorgan's)
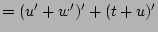 (identities & DeMorgan's)
(identities & DeMorgan's)
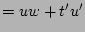 (DeMorgan's once again)
(DeMorgan's once again)
u \& w | ~t \& ~u
-
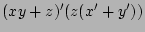
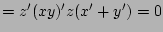 (DeMorgan's and identity)
(DeMorgan's and identity)
-
![$[(x+a)(x+b)(x+c)(x+d)]'$](img37.png)
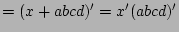 (Distributive & DeMorgan's)
(Distributive & DeMorgan's)
~x \& ~(a \& b \& c \& d)
MM Hugue
2008-01-27