Gates: XOR properties

Truth table:

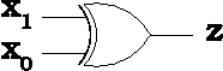
Symbol:

Input

Output

x0

x1

z

0

0

0

0

1

1

1

0

1

1

1

0

XOR can be expressed in terms of AND, OR, NOT:

x XOR y == ( x AND (NOT y) ) OR ( (NOT x) AND y )

(If x is true, y must be false, and vice versa.)

x0 ^ x1 ^ . . . xn

is true if the number of true values is odd,

and false if the number of true values is even.  Why?

x0 ^ x1 ^ . . . xn == (x0 + x1 + . . . xn) % 2

XOR is the same as the sum modulo 2

x ^ 0 = x

XORing with 0 gives you back the same number (identity)

x ^ 1 = ~x

XORing with 1 gives you the complement

x ^ x = 0

XORing a number with itself gives 0