Answer: See notes for correct picture; circuit has four inputs:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . The proper output is determined by the
(decimal) value of the two select inputs:
. The proper output is determined by the
(decimal) value of the two select inputs: ![]() ,
, ![]() . The function
table is given below:
. The function
table is given below:
| output | ||
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Answer: True Proof: matching truth tables works. Or, use Boolean identities on the left hand side of the equation above to get:
Remember, we have commutativity and associativity of or and and; also, the 'or' of 1 with anything else is 1.
Answer: The trick here is to us DeMorgan's law, which permits you to derive an equivalent expression: (A or (not B)). Thus, in one expression you can use one OR gate and one inverter. In the other, as originally written, you use an AND gate, and two inverters.
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
- the number of lines in a truth
table for a combinational circuit having 6 inputs.
Answer: Given 6 variables, each with two values, gives you
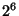 rows.
rows.
- the number of of possible combinational circuits having 6
inputs and one (1) output. (Hint: to avoid double jeopardy, you may
assume that V is the number of rows in a 6 input truth table.)
Answer: You need the number of rows in the truth table to get this right; so, rather than make the two pieces coupled, you can use the variable V for the number of rows in the truth table, as we shall do here at first. We have V rows in the truth table and one output, call it W. There are two possible output values associated with each row of the truth table; this gives
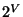 possible outputs, since V is the number of
rows. Substituting from the first part gives us
possible outputs, since V is the number of
rows. Substituting from the first part gives us 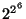 possible one
output combinational circuits given 6 inputs.
possible one
output combinational circuits given 6 inputs.
Answer: The easiest way to see this is to design the part. Since it is a strict encoder, exactly one bit in the input can be non-zero. The truth table is shown below:
| W | ||
| 0 | 1 | 0 |
| 1 | 0 | 1 |
A Boolean expression which satisfies this truth table is ![]() ,
meaning that no gates are involved; the output merely corresponds to
the value of input
,
meaning that no gates are involved; the output merely corresponds to
the value of input ![]() , and anyone can connect that input directly
to the output-no such part is ever needed.
, and anyone can connect that input directly
to the output-no such part is ever needed.