


Next: About this document ...
Up: sam2
Previous: Problem 2:``Stilgar's Self-Adjusting Structures
Last, but not least, shorter focused topic questions.
They are tailored
to a variety of skills; so, don't panic until after you've read them all.
DO any 8 of the TEN problems here--that's right, you can skip TWO (2)!
- (6) 3.1
- Derive a minimum cost spanning tree for the following
undirected
graph, where the weights are listed after the edge. For example, the
weight of the edge (A,B) is given by 2.
For full credit, explain how you know that you have achieved a minimum?
| Vertex |
Edges |
|
|
|
|
| A |
 A,B A,B (2) (2) |
 A,C A,C (1) (1) |
 A,D A,D (3) (3) |
 A,E A,E (2) (2) |
 A,F A,F (4) (4) |
| B |
 B,A B,A (2) (2) |
 B,C B,C (4) (4) |
 B,D B,D (4) (4) |
 B,G B,G (2) (2) |
|
| C |
 C,A C,A (1) (1) |
 C,B C,B (4) (4) |
 C, F C, F (1) (1) |
|
|
| D |
 D,A D,A (3) (3) |
 D,B D,B (4) (4) |
 D, E D, E (3) (3) |
|
|
| E |
 E,A E,A (2) (2) |
 E,D E,D (3) (3) |
 E,G E,G (2) (2) |
|
|
| F |
 F,A F,A (4) (4) |
 F,C F,C (1) (1) |
 F,G F,G (5) (5) |
|
|
| G |
 G,B G,B (2) (2) |
 G,E G,E (2) (2) |
 G,F G,F (5) (5) |
|
|
- (6) 3.2
- What is meant by the term amortized
analysis? Why might this method be preferred over asymptotic analysis
for some applications?
- (6) 3.3
- What is the buddy algorithm?
Give a definition of the buddy algorithm, and identify a benefit and a
drawback of using it.
- (6) 3.4
- Each of the functions below has been proposed as a hashing
function to
map an integer key
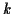 to a hash table of of size
to a hash table of of size 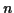 . Evaluate them for their
acceptability for insert and search operations, and explain the flaw or
benefit associated with each. That is, why is it acceptable, or why it is
not acceptable.
. Evaluate them for their
acceptability for insert and search operations, and explain the flaw or
benefit associated with each. That is, why is it acceptable, or why it is
not acceptable.
- A.
-
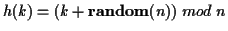 , where
, where
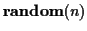 is
a randomly generated integer from the interval
is
a randomly generated integer from the interval ![$[0, n-1]$](img13.gif) inclusive, and
inclusive, and
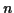 is a prime number.
is a prime number.
- B.
-
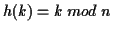 , where
, where 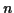 is a power of 2.
is a power of 2.
- (6) 3.5
- Sparse matrix schemes are only beneficial if the sparse representation
takes less space than the entire matrix, including the explicit zeros, as this
problem illustrates.
Assume that a sparse n x n matrix contains k non-zero
integers.
Describe and draw a storage scheme that takes advantage of
sparseness, and determine the cut-off value of k for your scheme.
That is, determine the first value of k for
which the sparse storage requirements exceed the space needed for the
entire n x n matrix.
- (6) 3.6
- Explain in words
how to perform
a breadth first traversal algorithm of the
graph G(V,E) using start vertex,
 .
.
- (6) 3.7
- Explain why merge-sort is in
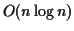 , and indicate what
data structure should be used to make this algorithm space efficient.
You are welcomed to use an example to show how the algorithm works-no
fancy definition or proof required.
, and indicate what
data structure should be used to make this algorithm space efficient.
You are welcomed to use an example to show how the algorithm works-no
fancy definition or proof required.
- (6) 3.8
- In the context of the project,
briefly explain an algorithm for finding the closest base
to a given raw material site. For full credit, explain why the algorithm is
better than a brute force search of all possible bases.
- (6) 3.9
- In the context of the project, suppose that you were
required to support continuous access to the data in the PM1 quadtree. That
is, you should be able to satisfy any of the project functions that use the
quad tree,
while inserting or deleting sites and paths.
However, you must use current data if at
all possible, meaning, for example,
that as soon as a pending insert has finished, any
function initiated thereafter must be able to access that site.
How would you modify your project code or operation
to support this new constraint?
- (6) 3.10
- Suppose a depth first search (dfs) algorithm is performed on the graph
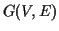 , where the number of vertices is
, where the number of vertices is 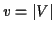 , and the number of edges
is
, and the number of edges
is 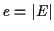 . Let
. Let 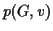 be the number of vertices visited by dfs.
Initialize
be the number of vertices visited by dfs.
Initialize 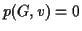 , and add 1 to
, and add 1 to 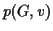 every time the dfs
algorithm examines a vertex, thus counting the examination of a
vertex that has been seen before as a visit, which
happens in the case of cycles.
every time the dfs
algorithm examines a vertex, thus counting the examination of a
vertex that has been seen before as a visit, which
happens in the case of cycles.
Since the algorithm must examine each vertex at least once, we have
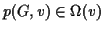 . Is
. Is
 ? If not, explain why not.
If so, explain why, and give a estimate
of the worst case value of the growth constant
? If not, explain why not.
If so, explain why, and give a estimate
of the worst case value of the growth constant 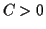 for which
for which
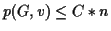 when
when 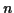 is large enough .
is large enough .



Next: About this document ...
Up: sam2
Previous: Problem 2:``Stilgar's Self-Adjusting Structures
MM Hugue
2001-03-11
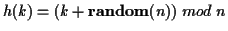 , where
, where
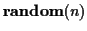 is
a randomly generated integer from the interval
is
a randomly generated integer from the interval ![$[0, n-1]$](img13.gif) inclusive, and
inclusive, and
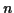 is a prime number.
is a prime number.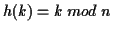 , where
, where 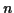 is a power of 2.
is a power of 2.
![]() . Is
. Is
![]() ? If not, explain why not.
If so, explain why, and give a estimate
of the worst case value of the growth constant
? If not, explain why not.
If so, explain why, and give a estimate
of the worst case value of the growth constant ![]() for which
for which
![]() when
when ![]() is large enough .
is large enough .