


Next: About this document ...
Homework 4: Pivots, Partitions, and Sorting
Handed out Wednesday, November 2. Due at the start of class Thursday, November 8.
- Problem 1.
- Consider the following recurrence with
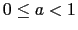 and
and 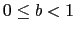 , and
, and 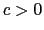 .
.
- (a)
- Show that
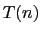 is bounded above by a linear function when
is bounded above by a linear function when 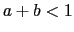 .
.
- (b)
- Show that
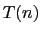 is in
is in 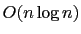 when
when 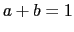 .
.
- Problem 2.
- For each of the following sorting algorithms, derive the
asymptotic
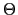 running time given that the input array is
given in reverse sorted order (that is, they keys appear in
decreasing order in the initial array). You may assume all the
elements are distinct. In each case briefly explain your answer,
but a formal proof is not required.
running time given that the input array is
given in reverse sorted order (that is, they keys appear in
decreasing order in the initial array). You may assume all the
elements are distinct. In each case briefly explain your answer,
but a formal proof is not required.
- (a)
- MergeSort.
- (b)
- HeapSort.
- (c)
- QuickSort. (Rather than picking the pivot at random,
assume that the pivot is deterministically chosen to be the first
element in the subarray, that is,
![$A[p]$](img10.png) .)
.)
- Problem 3.
- Give a
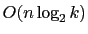 -time algorithm to merge
-time algorithm to merge 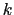 sorted lists into one sorted list, where
sorted lists into one sorted list, where 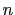 is the number of
elements in all the input lists. You may explain
your algorithm at a high level. Briefly explain how your algorithm
works and derive its running time. (Hint: Use a heap for the
k-way merging.)
is the number of
elements in all the input lists. You may explain
your algorithm at a high level. Briefly explain how your algorithm
works and derive its running time. (Hint: Use a heap for the
k-way merging.)
- Problem 4.
- You are given an array of
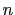 keys, each with one of
the values red, white, and blue. Give an
keys, each with one of
the values red, white, and blue. Give an 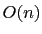 algorithm for ``sorting'' the keys so that all the reds come
before all the whites, and all the whites come before
all the blues. The only operations permitted are examination
of a key to find out what color it is (ie,
algorithm for ``sorting'' the keys so that all the reds come
before all the whites, and all the whites come before
all the blues. The only operations permitted are examination
of a key to find out what color it is (ie, if (keys[i] == Red)),
and swap of two keys specified by their indices (Swap(i, j)).
That is to say, you may not create any additional arrays!
Give psuedocode for your algorithm and derive its running time.



Next: About this document ...
Gregory Benjamin
2011-11-01
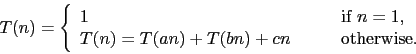
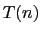 is bounded above by a linear function when
is bounded above by a linear function when 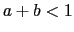 .
.
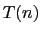 is in
is in 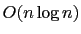 when
when 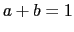 .
.
![$A[p]$](img10.png) .)
.)