


Next: About this document ...
Homework 3: Recurrences and Sorting
Handed out Wednesday, October 19. Due at the start of class Tuesday, November 1.
- Problem 1.
- Rank the following functions in increasing order of asymptotic growth rate.
For functions that are asymptotically equivalent, group them together. You
do not need to prove your ordering, but you may supply explanations for the
purpose of getting partial credit. (Note that all logs with unspecified bases
are assumed to be a log base 2.)
- Problem 2.
- A QM Sort is based on
the Merge Sort alogorithm discussed in class and in Lecture 6 of
Dr. Mount's notes. The difference between QM Sort and Merge Sort is
that we split the current list into 5 pieces during the divide
stage.
- a.
- Write the pseudocode for QM sort, using the code
in lecture 6 as a model.
- b.
- Derive a recurrence equation for the time required to sort
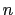 elements.
elements.
- c.
- Solve the recurrence for QM sort using the iteration method or the rrecurrence tree table, assuming that
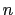 is a power of 5.
is a power of 5.
- d.
- Is QM sort stable? If not, give an example to illustrate your answer. If so, explain why stability is guaranteed.
- Problem 3.
- Selection Sort can be thought of as a recursive alogorithm
as follows:
Find the largest element and put it at the end of the list (to be sorted).
Recursively sort the remaining elements.
- a.
- Write down the recursive version of Selection Sort in psuedocode.
- b.
- Derive a recurrence for the exact number of comparisons that your alogorithm uses.
- c.
- Use the iteration method or a recurrence tree to solve the recurrence.
Simplify as much as possible.
- Problem 4.
- This problem uses a more Ambitious version of Master Theorem (AMT):
implies
Please solve the following recurrences exactly using the above version
of the theorem, or if you cannot use the Ambitious Master Theorem (AMT) to do so, explain why.
You should assume that 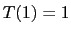 unless otherwise stated.
unless otherwise stated.
- (a)
-
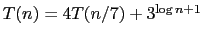 .
.
- (b)
-
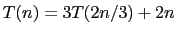 .
.
- (c)
-
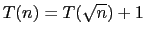 , and
, and 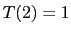 .
.
- (d)
-
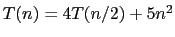 .
.
- (e)
-
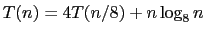 .
.
- Problem 5.
- Use iteration or a recurrence tree to solve (exactly) all of the recurrences of the previous
problem which you could not solve by the AMT. In all cases
you may make whatever simplifying assumptions you want about
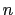 . You may
also assume that
. You may
also assume that 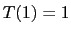 . (In part (c) it is convenient to assume that
. (In part (c) it is convenient to assume that
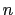 is of the form
is of the form 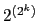 for some
for some  , and that
, and that 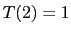 .)
.)



Next: About this document ...
Gregory Benjamin
2011-11-01
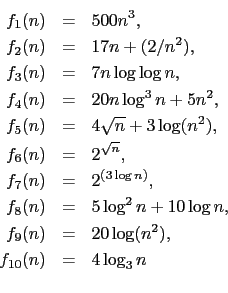
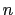 elements.
elements.
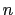 is a power of 5.
is a power of 5.
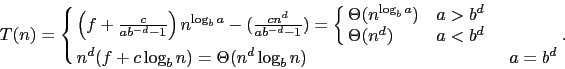
![]() unless otherwise stated.
unless otherwise stated.
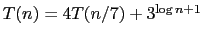 .
.
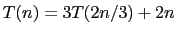 .
.
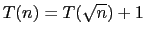 , and
, and 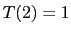 .
.
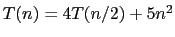 .
.
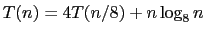 .
.