- (a)
-
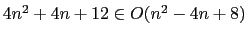
- (b)
-
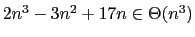 .
.
- (c)
-
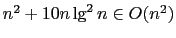 . (Hint: Find
. (Hint: Find 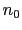 such that
such that
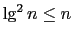 , for all
, for all 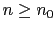 .)
.)
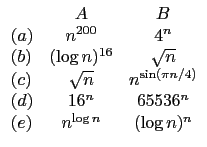
for i= 1 to n-1 do
base_j = i;
base_x = Keys[i]
for j = i + 1 to n do
If Keys[j] < base_x then
base_j = j;
base_x = Keys[j];
end forj;
If base_j < > i then
Keys[base_j] = Keys[i];
Keys[i] =base_x;
end fori;
- (a)
- Give a summation for the number of key swaps
in the worst case and simplify your summation.
- (b)
- Give a summation for the number of key swaps
in the best case and simplify your summation.
- (c)
- Give a double summation for the number of comparisons in the worst case and simplify your summation.
- (d)
- Give a double summation for the number of comparisons in the best case and simplify your summation.
- (e)
- Give a double summation for the number of comparisons in the average case, but do not solve.