Department of
Computer Science |
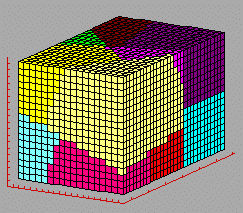
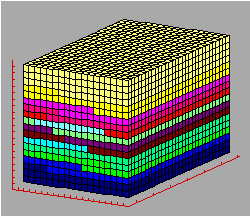
Simulations for DSMCIn highly adaptive irregular problems such as many Particle-In-Cell (PIC) codes and Direct Simulation Monte Carlo (DSMC) codes, data access patterns may vary from time step to time step. To efficiently parallelize such adaptive irregular problems on distributed memory parallel computers, ... effective methods for domain partitioning ... must be addressed. A simple one-dimensional domain partitioning method is implemented and compared with unstructured mesh partitioners such as recursive coordinate bisection and recursive inertial bisection. DemosRecursive coordinate bisection (RCB)(Click here to view the animation) There have been several theoretical and experimental discussions of partitioning strategies based on spatial information for many years. Recursive coordinate bisection (RCB) is a well-known algorithm which bisects a problem domain into two pieces of equal work load recursively until the number of subdomains is equal to the number of processors. Recursive inertial bisection (RIB)(Click here to view the animation) Recursive inertial bisection (RIB) is similar to RCB in that it bisects a problem domain recursively based on spatial information, but RIB uses minimum moment of inertia when it selects bisectioning directions, whereas RCB selects bisectioning directions from x-, y-, or z-dimensions. In other words, RIB bisects a 3-dimensional domain with a plane at any angle with respect to the coordinate axes, whereas RCB does so only with a plane perpendicular to one of the x, y and z coordinate axes. Clearly the number of processors has to be a power of 2 to apply these algorithms on parallel computers. Chain(Click here to view the animation) Chain partitioners decompose a chain-structured problem domain whose task
graph is a chain of work units into a set of pieces which satisfies contiguity constraints
-- each processor has a contiguous subdomain of work units assigned to it. That is, a
problem domain has to be partitioned in such a way that work units i and i+1 are assigned
to the same or to adjacent processors. Relatively simple algorithms for finding the
optimal partition of a chain-structured problem have been suggested. While these
algorithms are developed to optimize computation and communication costs at the same time,
we have developed and used a new chain partitioning algorithm which considers computation
cost only. This algorithm requires only one step of global communication and a few steps
of local computation. |
|