CMSC 351 - "Thought Questions" - CMSC 351
Not Graded but Should be Done
(1) Solve the following precisely to determine the expected
runtime of Insertion Sort.
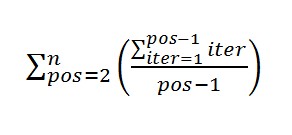 (2) The best case scenario for Insertion Sort is that as we move "left"
through the positions in the array inserting the next value into the
already-sorted "right" side of the array, then we discover that value
is already in the correct place (1 comparison).
The worst case scenario for Insertion Sort is that as we move "left"
through the positions in the array inserting the next value into the
already-sorted "right" side of the array, the we discover that value
is actually as far from the right place as possible (pos-1 comparisons).
Imagine a situation where each "next" value is 25% of the size of the
already-sorted side away from its correct spot. Calculate the runtime
of the algorithm for that scenario.
Core of solution to #2
(3) Imagine you were told that the input list you were going to be given
for a sorting problem had the following interesting property:
* for each item in the list, its value is within the
middle third of the values that are "to the left of it"
(a) how could you modify the Insertion Sort algorithm to take
advantage of this to reduce the number of comparisons used?
part (a) solution
(b) how would this impact the worst-case runtime?
part (b) solution
(4) I have an algorithm that is recursive and does the following:
- if the input list has 1 element, it does one step of WORK
and then returns its answer
- if the input list is larger than 1 element, the algorithm
performs a partitioning of the list into two lists which
requires (list.length)^2 steps of WORK, and then recursively
calls itself on the larger of the two lists
Set things up to formally prove (using constructive induction to
determine a value for c and for n0) that the expected amount of
work that the algorithm will perform on a list of size n
(assuming that all sized "splits" of the list are equally likely
as a result of the partitioning) will be O(n3).
NOTE: Typo fixed on morning of 3/12. Was meant to ask O(n3).
summation ready for constructive induction
(5) Assume you are doing randomized median finding, but that by a quirk of
nature, the randomly chosen pivot value is always the 1/3rd-smallest
item in the list. Build a summation representing the worst-case runtime
of this scenario, and solve it.
recurrence for #5 from which you use the tree technique
(6) Assume that we are using random pivot point selection within the
Quicksort algorithm. Also assume that by luck, we end up always
having that randomly chosen pivot be roughly the n/4th smallest
element in the list (give or take one position).
Build and then solve the summation representing the number of
comparisons done in this scenario in a way that will reveal as
much information as possible about the highest-order term and
any constant multiplier associated with it.
recurrence for #6 from which you use the tree technique
(7) Assume that we are using random pivot point selection within the
Quicksort algorithm. Also this time that our luck is very weird
such that every other time we do a partitioning we alternate
back and forth between randomly picking the largest value in the
list we are given and the median value of the list we are given.
Draw a tree representing this and look for a way to create a
summation that represents the number of comparisons done in this
scenario for a general n sized input.
hints about the tree for #7
(8) In class our average case analysis for Quicksort took us to having
a summation that we needed to slightly overestimate. One way to do
this would be to set the log base to "e" and therefore being able
to use the integral bound.
(2) The best case scenario for Insertion Sort is that as we move "left"
through the positions in the array inserting the next value into the
already-sorted "right" side of the array, then we discover that value
is already in the correct place (1 comparison).
The worst case scenario for Insertion Sort is that as we move "left"
through the positions in the array inserting the next value into the
already-sorted "right" side of the array, the we discover that value
is actually as far from the right place as possible (pos-1 comparisons).
Imagine a situation where each "next" value is 25% of the size of the
already-sorted side away from its correct spot. Calculate the runtime
of the algorithm for that scenario.
Core of solution to #2
(3) Imagine you were told that the input list you were going to be given
for a sorting problem had the following interesting property:
* for each item in the list, its value is within the
middle third of the values that are "to the left of it"
(a) how could you modify the Insertion Sort algorithm to take
advantage of this to reduce the number of comparisons used?
part (a) solution
(b) how would this impact the worst-case runtime?
part (b) solution
(4) I have an algorithm that is recursive and does the following:
- if the input list has 1 element, it does one step of WORK
and then returns its answer
- if the input list is larger than 1 element, the algorithm
performs a partitioning of the list into two lists which
requires (list.length)^2 steps of WORK, and then recursively
calls itself on the larger of the two lists
Set things up to formally prove (using constructive induction to
determine a value for c and for n0) that the expected amount of
work that the algorithm will perform on a list of size n
(assuming that all sized "splits" of the list are equally likely
as a result of the partitioning) will be O(n3).
NOTE: Typo fixed on morning of 3/12. Was meant to ask O(n3).
summation ready for constructive induction
(5) Assume you are doing randomized median finding, but that by a quirk of
nature, the randomly chosen pivot value is always the 1/3rd-smallest
item in the list. Build a summation representing the worst-case runtime
of this scenario, and solve it.
recurrence for #5 from which you use the tree technique
(6) Assume that we are using random pivot point selection within the
Quicksort algorithm. Also assume that by luck, we end up always
having that randomly chosen pivot be roughly the n/4th smallest
element in the list (give or take one position).
Build and then solve the summation representing the number of
comparisons done in this scenario in a way that will reveal as
much information as possible about the highest-order term and
any constant multiplier associated with it.
recurrence for #6 from which you use the tree technique
(7) Assume that we are using random pivot point selection within the
Quicksort algorithm. Also this time that our luck is very weird
such that every other time we do a partitioning we alternate
back and forth between randomly picking the largest value in the
list we are given and the median value of the list we are given.
Draw a tree representing this and look for a way to create a
summation that represents the number of comparisons done in this
scenario for a general n sized input.
hints about the tree for #7
(8) In class our average case analysis for Quicksort took us to having
a summation that we needed to slightly overestimate. One way to do
this would be to set the log base to "e" and therefore being able
to use the integral bound.
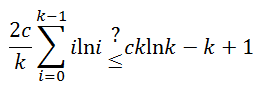 is what we are trying to prove. We know that
is what we are trying to prove. We know that
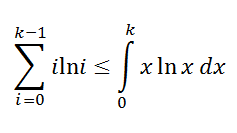 We then need to integrate x ln x dx. The soluton to that can be
seen here if you want to check your work.
Once we have that, we are ready to go forward, but we have a potential
problem with ln(0) since it's undefined, but since that came from T(0)
and we know T(0)=0, we can just remove that from our problem.
So, we are left needing to prove whether
We then need to integrate x ln x dx. The soluton to that can be
seen here if you want to check your work.
Once we have that, we are ready to go forward, but we have a potential
problem with ln(0) since it's undefined, but since that came from T(0)
and we know T(0)=0, we can just remove that from our problem.
So, we are left needing to prove whether
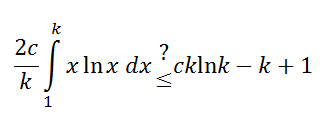 Use the result of your integration of x ln x dx to prove that.
(9) Let's assume that Median of Median-5s takes 25n in the worst case.
Using this, what would the worst-case runtime of Quicksort be if we
modified it to use the median as the pivot for each round?
(10)
log3(n)-1
Solve Σ (3/4)i
i=0
as precisely as possible, and then when you get to the very
end and have an "unusual" value, determine the constants that
you can guarantee bound it.
Solution for #10
(11) Given the recurrence:
T(1) = 0
T(n) = n2+T(n/2)
use the recurrence tree technique to create a summation representing
the runtime, then solve it precisely.
tree/work-per-level summation
Use the result of your integration of x ln x dx to prove that.
(9) Let's assume that Median of Median-5s takes 25n in the worst case.
Using this, what would the worst-case runtime of Quicksort be if we
modified it to use the median as the pivot for each round?
(10)
log3(n)-1
Solve Σ (3/4)i
i=0
as precisely as possible, and then when you get to the very
end and have an "unusual" value, determine the constants that
you can guarantee bound it.
Solution for #10
(11) Given the recurrence:
T(1) = 0
T(n) = n2+T(n/2)
use the recurrence tree technique to create a summation representing
the runtime, then solve it precisely.
tree/work-per-level summation
Web Accessibility
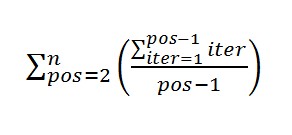 (2) The best case scenario for Insertion Sort is that as we move "left"
through the positions in the array inserting the next value into the
already-sorted "right" side of the array, then we discover that value
is already in the correct place (1 comparison).
The worst case scenario for Insertion Sort is that as we move "left"
through the positions in the array inserting the next value into the
already-sorted "right" side of the array, the we discover that value
is actually as far from the right place as possible (pos-1 comparisons).
Imagine a situation where each "next" value is 25% of the size of the
already-sorted side away from its correct spot. Calculate the runtime
of the algorithm for that scenario.
Core of solution to #2
(3) Imagine you were told that the input list you were going to be given
for a sorting problem had the following interesting property:
* for each item in the list, its value is within the
middle third of the values that are "to the left of it"
(a) how could you modify the Insertion Sort algorithm to take
advantage of this to reduce the number of comparisons used?
part (a) solution
(b) how would this impact the worst-case runtime?
part (b) solution
(4) I have an algorithm that is recursive and does the following:
- if the input list has 1 element, it does one step of WORK
and then returns its answer
- if the input list is larger than 1 element, the algorithm
performs a partitioning of the list into two lists which
requires (list.length)^2 steps of WORK, and then recursively
calls itself on the larger of the two lists
Set things up to formally prove (using constructive induction to
determine a value for c and for n0) that the expected amount of
work that the algorithm will perform on a list of size n
(assuming that all sized "splits" of the list are equally likely
as a result of the partitioning) will be O(n3).
NOTE: Typo fixed on morning of 3/12. Was meant to ask O(n3).
summation ready for constructive induction
(5) Assume you are doing randomized median finding, but that by a quirk of
nature, the randomly chosen pivot value is always the 1/3rd-smallest
item in the list. Build a summation representing the worst-case runtime
of this scenario, and solve it.
recurrence for #5 from which you use the tree technique
(6) Assume that we are using random pivot point selection within the
Quicksort algorithm. Also assume that by luck, we end up always
having that randomly chosen pivot be roughly the n/4th smallest
element in the list (give or take one position).
Build and then solve the summation representing the number of
comparisons done in this scenario in a way that will reveal as
much information as possible about the highest-order term and
any constant multiplier associated with it.
recurrence for #6 from which you use the tree technique
(7) Assume that we are using random pivot point selection within the
Quicksort algorithm. Also this time that our luck is very weird
such that every other time we do a partitioning we alternate
back and forth between randomly picking the largest value in the
list we are given and the median value of the list we are given.
Draw a tree representing this and look for a way to create a
summation that represents the number of comparisons done in this
scenario for a general n sized input.
hints about the tree for #7
(8) In class our average case analysis for Quicksort took us to having
a summation that we needed to slightly overestimate. One way to do
this would be to set the log base to "e" and therefore being able
to use the integral bound.
(2) The best case scenario for Insertion Sort is that as we move "left"
through the positions in the array inserting the next value into the
already-sorted "right" side of the array, then we discover that value
is already in the correct place (1 comparison).
The worst case scenario for Insertion Sort is that as we move "left"
through the positions in the array inserting the next value into the
already-sorted "right" side of the array, the we discover that value
is actually as far from the right place as possible (pos-1 comparisons).
Imagine a situation where each "next" value is 25% of the size of the
already-sorted side away from its correct spot. Calculate the runtime
of the algorithm for that scenario.
Core of solution to #2
(3) Imagine you were told that the input list you were going to be given
for a sorting problem had the following interesting property:
* for each item in the list, its value is within the
middle third of the values that are "to the left of it"
(a) how could you modify the Insertion Sort algorithm to take
advantage of this to reduce the number of comparisons used?
part (a) solution
(b) how would this impact the worst-case runtime?
part (b) solution
(4) I have an algorithm that is recursive and does the following:
- if the input list has 1 element, it does one step of WORK
and then returns its answer
- if the input list is larger than 1 element, the algorithm
performs a partitioning of the list into two lists which
requires (list.length)^2 steps of WORK, and then recursively
calls itself on the larger of the two lists
Set things up to formally prove (using constructive induction to
determine a value for c and for n0) that the expected amount of
work that the algorithm will perform on a list of size n
(assuming that all sized "splits" of the list are equally likely
as a result of the partitioning) will be O(n3).
NOTE: Typo fixed on morning of 3/12. Was meant to ask O(n3).
summation ready for constructive induction
(5) Assume you are doing randomized median finding, but that by a quirk of
nature, the randomly chosen pivot value is always the 1/3rd-smallest
item in the list. Build a summation representing the worst-case runtime
of this scenario, and solve it.
recurrence for #5 from which you use the tree technique
(6) Assume that we are using random pivot point selection within the
Quicksort algorithm. Also assume that by luck, we end up always
having that randomly chosen pivot be roughly the n/4th smallest
element in the list (give or take one position).
Build and then solve the summation representing the number of
comparisons done in this scenario in a way that will reveal as
much information as possible about the highest-order term and
any constant multiplier associated with it.
recurrence for #6 from which you use the tree technique
(7) Assume that we are using random pivot point selection within the
Quicksort algorithm. Also this time that our luck is very weird
such that every other time we do a partitioning we alternate
back and forth between randomly picking the largest value in the
list we are given and the median value of the list we are given.
Draw a tree representing this and look for a way to create a
summation that represents the number of comparisons done in this
scenario for a general n sized input.
hints about the tree for #7
(8) In class our average case analysis for Quicksort took us to having
a summation that we needed to slightly overestimate. One way to do
this would be to set the log base to "e" and therefore being able
to use the integral bound.
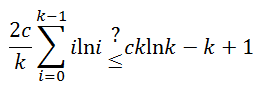 is what we are trying to prove. We know that
is what we are trying to prove. We know that
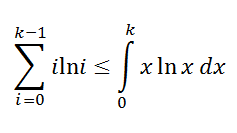 We then need to integrate x ln x dx. The soluton to that can be
seen here if you want to check your work.
Once we have that, we are ready to go forward, but we have a potential
problem with ln(0) since it's undefined, but since that came from T(0)
and we know T(0)=0, we can just remove that from our problem.
So, we are left needing to prove whether
We then need to integrate x ln x dx. The soluton to that can be
seen here if you want to check your work.
Once we have that, we are ready to go forward, but we have a potential
problem with ln(0) since it's undefined, but since that came from T(0)
and we know T(0)=0, we can just remove that from our problem.
So, we are left needing to prove whether
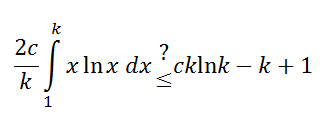 Use the result of your integration of x ln x dx to prove that.
(9) Let's assume that Median of Median-5s takes 25n in the worst case.
Using this, what would the worst-case runtime of Quicksort be if we
modified it to use the median as the pivot for each round?
(10)
log3(n)-1
Solve Σ (3/4)i
i=0
as precisely as possible, and then when you get to the very
end and have an "unusual" value, determine the constants that
you can guarantee bound it.
Solution for #10
(11) Given the recurrence:
T(1) = 0
T(n) = n2+T(n/2)
use the recurrence tree technique to create a summation representing
the runtime, then solve it precisely.
tree/work-per-level summation
Use the result of your integration of x ln x dx to prove that.
(9) Let's assume that Median of Median-5s takes 25n in the worst case.
Using this, what would the worst-case runtime of Quicksort be if we
modified it to use the median as the pivot for each round?
(10)
log3(n)-1
Solve Σ (3/4)i
i=0
as precisely as possible, and then when you get to the very
end and have an "unusual" value, determine the constants that
you can guarantee bound it.
Solution for #10
(11) Given the recurrence:
T(1) = 0
T(n) = n2+T(n/2)
use the recurrence tree technique to create a summation representing
the runtime, then solve it precisely.
tree/work-per-level summation