CMSC 652 Complexity Theory, Fall 2017
Course Description
Computational complexity theory studies the power of computation in terms of consumed computational resources such as time, memory, communication, number of rounds of communication, and randomness. It deals with fundamental questions such as:
Are algorithms that are given more time always able to solve more problems?
Is verifying solutions to problems easier than coming up with such solutions?
Can tossing coins help us compute faster?
Can we define randomness?
Is finding approximate answers easier than finding exact answers?
Can we prove that some interesting problems cannot be solved efficiently?
Can you verify that an algorithm solves a problem without solving it yourself?
This course is an introductory graduate-level course in computational complexity theory. No prior knowledge in complexity theory is assumed, except that it is assumed students are familiar and comfortable with the notions of Turing machines, languages, classes, P/NP, and NP-completeness (which will be reviewed quickly in the first week). On the other hand, the course will cover some fairly advanced (and abstract) material at a relatively quick pace; therefore, it is assumed that (1) students have “mathematical maturity” (e.g., are comfortable with proofs and abstract reasoning); (2) students are interested in the material; and (3) students are willing to spend time outside of class in order to better understand the material presented in class.
A tentative list of covered topics includes basic time and space complexity classes (e.g., P, NP, PSPACE, polynomial hierarchy), randomized computation, interactive proof systems, as well as more advanced topics such as the PCP theorem, circuit lower bounds, and pseudo-randomness.
If you are unsure whether this class is appropriate for you, you are recommended to look at the Arora and Barak textbook (as well as the previous offerings of the course) to see whether you (a) find the topics interesting, and (b) find the level of difficulty appropriate.
Generics
Prerequisite: CMSC 451, or CMSC 452, or Permission of the instructor
Lectures: CMSC 652, Tu Th 2:00pm – 3:15pm, CSI 2120
Instructor: Prof. Xiaodi Wu
Office AVW 3257, Email: xwu (at) cs.umd.edu
(Please use “CMSC 652” as the prefix in the subject when emailing me.).Teaching Assistant: Sheng Yang, Email: styang (at) cs.umd.edu
Syllabus: check here
Office hours:
Wu: Tu Th 3:30pm – 4:30pm or by appointments, at AVW 3257.
Yang: W 2:30pm – 3:30pm, at AVW 3164.
Evaluation: class participation (2%), assignments (43%), mid-term (25%), and final (30%). Details in the policy page.
Assignments
Homework assignments must be submitted electronically to ELMS. (Anyone having trouble with electronic submissions should contact the instructor as soon as possible.) I highly recommend the use of 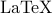 for the typesetting. Here is a good reference about the use of
for the typesetting. Here is a good reference about the use of 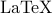 . Here is a latex template for writing solutions.
. Here is a latex template for writing solutions.
Assignment 0 due by 09/05/17. (tex).
Assignment 1 due by 09/14/17. (tex).
Assignment 2 due by 09/29/17. (tex).
Assignment 3 due by 10/13/17. (tex).
Assignment 4 due by 11/03/17. (tex).
Assignment 5 due by 11/17/17. (tex).
Assignment 6 due by 12/01/17. (tex).
Project Assignment (assignment 7): part (a) due by 11/05/17; part (b) due by 12/07/17. (tex)
Textbooks & Lectures
We will follow the text by Arora and Barak, supplemented with lecture notes giving further details or covering topics not in that text. It will be similar to the previous offering (by Prof Gasarch (Spring 2014), by Prof Katz (Fall 2011), and by Prof Srinivasan (Fall 2009). Recommended references include:
Sanjeev Arora and Boaz Barak. Complexity Theory: A Modern Approach
Oded Goldreich. Computational Complexity: A Conceptual Perspective
Useful resources include: Complexity Zoo.
Social Media
We use Piazza as the discussion forum. Piazza is FERPA-compliant in that it protects the privacy of students, keeps the information private, and is not searchable by search engines. In order to participate, all students are expected to register with an email address of their choice.
We use ELMS for submissions of assignments and exams and distributions of corresponding grades.
This website serves as the collection of information about the course, syllabus, handouts, and references. Please check frequently!